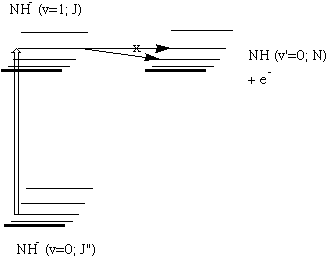Special
Announcements
The 2005
ACTC will be Held July 16-21, 2005
at UCLA and organized by Prof.
Emily Carter

This conference in Gyeongju,
Korea has a very international flavor and was quite exciting. It
honored Fritz Schaefer's 1000th publication (and his good
health).
What is Present Day
Theoretical Chemistry About?
|
Three Primary
Subdisciplines
|
|
|
A. Electronic structure theory
describes the motions of the electrons and produces energy
surfaces
The shapes and geometries of molecules, their electronic,
vibrational, and rotational energy levels and wavefunctions, as well
as the interactions of these states with electromagnetic fields lie
within the realm of structure theory.
1. The Underlying Theoretical Basis
In the Born-Oppenheimer
model of molecular structure, it is assumed that the electrons move
so quickly that they can adjust their motions essentially
instantaneously with respect to any movements of the heavier and
slower moving atomic nuclei. This assumption motivates us to view the
electrons moving in electronic wave functions (orbitals within the
simplest and most commonly employed theories) that smoothly "ride"
the molecule's atomic framework. These electronic functions are found
by solving a Schrödinger equation whose Hamiltonian
He contains the kinetic energy Te of the
electrons, the Coulomb repulsions among all the molecule's electrons
Vee, the Coulomb attractions Ven among the
electrons and all of the molecule's nuclei treated with these nuclei
held clamped, and the Coulomb repulsions Vnn among all of
these nuclei. The electronic wave functions yk
and energies Ek that result from solving the electronic
Schrödinger equation
He yk =
Ek yk
thus depend on the locations {Qi} at which the nuclei
are sitting. That is, the Ek and yk
are parametric functions of the coordinates of the nuclei.
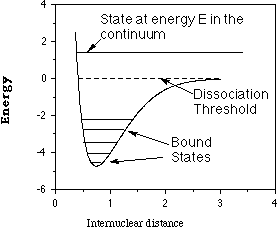
These electronic energies' dependence on the positions of the
atomic centers cause them to be referred to as electronic energy
surfaces such as that depicted below for a diatomic molecule where
the energy depends only on one interatomic distance R.
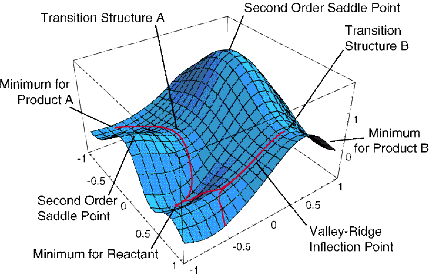
For non-linear polyatomic molecules having N atoms, the energy
surfaces depend on 3N-6 internal coordinates and thus can be very
difficult to visualize. A slice through such a surface (i.e., a plot
of the energy as a function of two out of 3N-6 coordinates) is shown
below and various features of such a surface are detailed.
The Born-Oppenheimer theory of molecular structure is soundly
based in that it can be derived from a starting point consisting of a
Schrödinger equation describing the kinetic energies of all
electrons and of all N nuclei plus the Coulomb potential energies of
interaction among all electrons and nuclei. By expanding the
wavefunction Y that is an eigenfunction of
this full Schrödinger equation in the complete set of functions
{ yk } and then neglecting all
terms that involve derivatives of any yk
with respect to the nuclear positions {Qi }, one can
separate variables such that:
1. The electronic wavefunctions and energies must obey
He yk =
Ek yk
2. The nuclear motion (i.e., vibration/rotation) wavefunctions
must obey
(TN + Ek) ck,L
= Ek,L ck,L
,
where TN is the kinetic energy operator for movement of
all nuclei.
That is, each and every electronic energy state, labeled k, has a
set, labeled L, of vibration/rotation energy levels Ek,L
and wavefunctions ck,L
.
Because the Born-Oppenheimer model is obtained from the full
Schrödinger equation by making approximations (e.g., neglecting
certain terms that are called non-adiabatic coupling terms), it is
not exact. Thus, in certain circumstances it becomes necessary to
correct the predictions of the Born-Oppenheimer theory (i.e., by
including the effects of the neglected non-adiabatic coupling terms
using perturbation theory).
For example, when developing a theoretical model to interpret the
rate at which electrons are ejected from rotationally/vibrationally
hot NH- ions, we
had to consider coupling between two states having the same
total energy:
1. 2P NH- in its
v=1 vibrational level and in a high rotational level (e.g., J >30)
prepared by laser excitation of vibrationally "cold" NH-
in v=0 having high J (due to natural Boltzmann populations);
see the figure below, and
2. 3S NH neutral plus an
ejected electron in which the NH is in its v=0 vibrational level (no
higher level is energetically accessible) and in various rotational
levels (labeled N).
Because NH has an electron affinity of 0.4 eV, the total energies
of the above two states can be equal only if the kinetic energy KE
carried away by the ejected electron obeys:
KE = Evib/rot (NH- (v=1, J)) -
Evib/rot (NH (v=0, N)) - 0.4 eV.
In the absence of any non-adiabatic coupling terms, these two
isoenergetic states would not be coupled and no electron detachment
would occur. It is only by the anion converting some of its
vibration/rotation energy and angular momentum into electronic energy
that the electron that occupies a bound N2p orbital in
NH- can gain enough energy to be ejected.
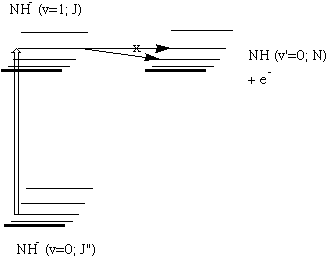
Energies of NH- and of NH pertinent to the
autodetachment of v=1, J levels of NH- formed by laser
excitation of v=0 J'' NH- .
My own research efforts
have, for many years, involved studying negative molecular ions (a
field in which Professor Ken
Jordan is a leading figure) taking into account such non
Born-Oppenheimer couplings, especially in cases where
vibration/rotation energy transferred to electronic motions causes
electron detachment as in the NH- case detailed above.

|
|

|
Professor Ken Jordan
|
|
- Professor Jack Simons
- in the Uinta Mts.
|
My good friend, Professor Yngve
Öhrn, has been active in attempting to avoid making the
Born-Oppeheimer approximation and, instead, treating the dynamical
motions of the nuclei and electrons simultaneously. Professor
David
Yarkony has contributed much to the recent
treatment of non-adiabatic (i.e., non Born-Oppenheimer) effects
and to the inclusion of spin-orbit coupling in such studies.
|

|
|

|
|
Professor Yngve Öhrn
|
|
Professor David Yarkony
|
2. What is Learned from an Electronic Structure
Calculation?
The knowledge gained via structure theory is great. The electronic
energies Ek (Q) allow one to determine (see my book
Energetic Principles of Chemical
Reactions) the geometries and relative energies of various
isomers that a molecule can assume by finding those geometries
{Qi ) at which the energy surface Ek has minima
 Ek
/
Ek
/ Qi
= 0, with all directions having positive curvature (this is
monitored by considering the so-called Hessian matrix
Qi
= 0, with all directions having positive curvature (this is
monitored by considering the so-called Hessian matrix 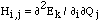 if none of its eigenvalues are negative, all directions have positive
curvature). Such geometries describe stable isomers, and the energy
at each such isomer geometry gives the relative energy of that
isomer. Professor Berny
Schlegel at Wayne State has been one of the leading figures
whose efforts are devoted to using gradient and Hessian information
to locate stable structures and transition states. Professor
Peter Pulay has
done as much as anyone to develop the theory that allows us to
compute the gradients and Hessians appropriate to the most commonly
used electronic structure methods. His group has also pioneered the
development of so-called local correlation methods which focus on
using localized orbitals to compute correlation energies in a manner
that scales less severely with system size than when delocalized
canonical molecular orbitals are employed.
if none of its eigenvalues are negative, all directions have positive
curvature). Such geometries describe stable isomers, and the energy
at each such isomer geometry gives the relative energy of that
isomer. Professor Berny
Schlegel at Wayne State has been one of the leading figures
whose efforts are devoted to using gradient and Hessian information
to locate stable structures and transition states. Professor
Peter Pulay has
done as much as anyone to develop the theory that allows us to
compute the gradients and Hessians appropriate to the most commonly
used electronic structure methods. His group has also pioneered the
development of so-called local correlation methods which focus on
using localized orbitals to compute correlation energies in a manner
that scales less severely with system size than when delocalized
canonical molecular orbitals are employed.

|
|

|
|
Professor Bernie Schlegel
|
|
Professor Peter Pulay
|
- There may be other geometries on the Ek energy
surface at which all "slopes" vanish
 Ek
/
Ek
/ Qi
= 0, but at which not all directions possess positive
curvature. If the Hessian matrix has only one negative eigenvalue
there is only one direction leading downhill away from the point
{Qi } of zero force; all the remaining directions lead
uphill from this point. Such a geometry describes that of a
transition state, and its energy plays a central role in
determining the rates of reactions which pass through this
transition state.
Qi
= 0, but at which not all directions possess positive
curvature. If the Hessian matrix has only one negative eigenvalue
there is only one direction leading downhill away from the point
{Qi } of zero force; all the remaining directions lead
uphill from this point. Such a geometry describes that of a
transition state, and its energy plays a central role in
determining the rates of reactions which pass through this
transition state.
At any geometry {Qi }, the gradient or slope vector
having components  Ek
/
Ek
/ Qi
provides the forces (Fi = -
Qi
provides the forces (Fi = -  Ek
/
Ek
/ Qi
) along each of the coordinates Qi . These forces
are used in molecular dynamics simulations (see the following
section) which solve the Newton F = m a equations and
in molecular mechanics studies which are aimed at locating those
geometries where the F vector vanishes (i.e., the stable
isomers and transition states discussed above).
Qi
) along each of the coordinates Qi . These forces
are used in molecular dynamics simulations (see the following
section) which solve the Newton F = m a equations and
in molecular mechanics studies which are aimed at locating those
geometries where the F vector vanishes (i.e., the stable
isomers and transition states discussed above).
Also produced in electronic structure simulations are the
electronic wavefunctions {yk }
and energies {Ek} of each of the electronic states. The
separation in energies can be used to make predictions about the
spectroscopy of the system. The wavefunctions can be used to evaluate
properties of the system that depend on the spatial distribution of
the electrons in the system. For example, the z- component of the
dipole moment of a molecule mz
can be computed by integrating the probability density for
finding an electron at position r multiplied by the z-
coordinate of the electron and the electron's charge e: mz
= Ú e yk*
yk z dr . The average kinetic energy of an
electron can also be computed by carrying out such an average-value
integral: Ú
yk* (-
h2 /2me  2
) yk dr. The rules
for computing the average value of any physical observable are
developed and illustrated in popular
undergraduate text books on physical chemistry (e.g., Atkins
text or Berry, Rice, and
Ross) and in graduate level texts (e.g., Levine,
McQuarrie, Simons and
Nichols).
2
) yk dr. The rules
for computing the average value of any physical observable are
developed and illustrated in popular
undergraduate text books on physical chemistry (e.g., Atkins
text or Berry, Rice, and
Ross) and in graduate level texts (e.g., Levine,
McQuarrie, Simons and
Nichols).

|
|

|
|
Professor Steve Berry, University of Chicago
one of the most broad-based members of the theory
community
|
|
Dr. Jeff Nichols, Oak Ridge National Labs
|

Prof. Stuart Rice, University of Chicago. He has done as much as
anyone in a tremendous variety of theoretical studies including
studies of interfaces and using coherent external perturbations to
control chemical processes.
Not only can electronic wavefunctions tell us about the average
values of all physical properties for any particular state (i.e.,
yk above), but they also allow
us to tell how a specific "perturbation" (e.g., an electric field in
the Stark effect, a magnetic field in the Zeeman effect, light's
electromagnetic fields in spectroscopy) can alter the specific state
of interest. For example, the perturbation arising from the electric
field of a photon interacting with the electrons in a molecule is
given within the so-called electric dipole approximation (see, for
example, Simons and Nichols, Ch.
14) by:
Hpert =Sj
e2 rj • E
(t)
where E is the electric field
vector of the light, which depends on time t in an oscillatory
manner, and ri is the vector denoting the spatial
coordinates of the ith electron. This perturbation,
Hpert acting on an electronic state yk
can induce transitions to other states yk'
with probabilities that are proportional to the square of the
integral
Ú
yk'* Hpert
yk dr .
So, if this integral were to vanish, transitions between
yk and
yk' would not occur, and
would be referred to as "forbidden". Whether such integrals vanish or
not often is determined by symmetry. For example, if yk
were of odd symmetry under a plane of symmetry sv
of the molecule, while yk' were
even under sv , then the
integral would vanish unless one or more of the three cartesian
components of the dot product rj • E were odd under
sv The general idea is that for
the integral to not vanish the direct product of the symmetries of
yk and of yk'
must match the symmetry of at least one of the symmetry components
present in Hpert . Professor Poul
Jørgensen has been especially involved in developing
such so-called response theories for perturbations that may be time
dependent (e.g., as in the interaction of light's electromagnetic
radiation).
3. Present Day Challenges in Structure
Theory
As a preamble to the following discussion, I wish to draw the
readers' attention to the web pages of several prominent theoretical
chemists who have made major contributions to the development and
applications of electronic structure theory and who have agreed to
allow me to cite them in this text. In addition to the people
specifically mentioned in this text for whom I have already provided
web links, I encourage you to look at the following web pages for
further information:

|
Professor Ernest
Davidson, Univ. of Washington and Indiana University
has contributed as much as anyone both to the development of
the fundamentals of electronic structure theory and its
applications to many perplexing problems in molecular
structure and spectroscopy.
|
|
The late Professor John
Pople, Northwestern University, made developments
leading to the suite of Gaussian computer codes that now
constitute the most widely used electronic structure
computer programs.His contributions to theory were
recognized in his sharing the 1998 Nobel Prize in
Chemistry.
|

|
|
Professor Bill
Goddard, Cal Tech. When most quantum chemists were
pursuing improvements in the molecular orbital method, he
returned to the valence bond theory and developed the
so-called GVB methods that allow electron correlation to be
included within a valence bond framework.
|
|
Professor Fritz
Schaefer, University of Georgia. He has carried out
as many applications of modern electronic structure theory
to important chemical problems as anyone.
|

|

|
Professor Rod
Bartlett, University of Florida. He brought the
coupled-cluster method, developed earlier by others, into
the mainstream of electronic structure theory.
|
Professor Bernd
Heb,
University of Erlangen, has a special focus
in his research on relativistic effects and the development of tools
needed to study them.

Professor Hans-Joachim
Werner, University of Stuttgart, has for many years pioneered
developments of multi-configurational SCF and coupled-cluster methods
and applied them to a wide variety of chemical problems.

Professor Sigrid
Peyerimhoff, Bonn University, is one of the earliest pioneers of
multi-reference configuration interaction methods and has applied
these powerful tools to many important chemical species and
reactions. She has prepared a wonderful web site that details much of
the history
of the development of quantum chemistry.

Professor Debashis
Mukherjee of the Indian Association for the Cultivation of
Science has extended the basis of coupled-cluster theory to allow for
multiconfigurational reference wavefunctions and for the calculation
of excitation energies and ionization energies.

|
The late Professor Mike
Zerner, University of Florida, was very influential in
continuing the development of semi-empirical methods within
quantum chemistry. Such methods can be applied to much
larger molecules than ab initio methods, so their continued
evolution is an essential component to growth in this field
of theoretical chemistry.
|

|
Professor Poul
Jørgensen of Aarhus University

spent much of his early career developing the fundamentals of
electron and polarization propagator theory. Following up on that
early work, he moved on to develop the tools of response theory (time
dependent and time independent) for computing a wide variety of
molecular properties. His group has combined the power of response
theory with several powerful wavefunctions including coupled-cluster
and configuration interaction functions.
a. Orbitals form the starting point; what are the
orbitals?
The full N-electron Schrödinger equation governing the
movement of the electrons in a molecule is
[-h2 /2me
Si=1  i2
- Sa Si
Za e2 /ria + Si,j
e2 /rij ] y
= E y .
i2
- Sa Si
Za e2 /ria + Si,j
e2 /rij ] y
= E y .
In this equation, i and j label the electrons and a labels the
nuclei. Even at the time this material was written, this equation had
been solved only for the case N=1 (i.e., for H, He+ ,
Li2+ , Be3+ , etc.). What makes the problem
difficult to solve for other cases is the fact that the Coulomb
potential e2/rij acting between pairs of
electrons depends upon the coordinates of the two electrons
ri and rj in a way that does not
allow the separations of variables to be used to decompose this
single 3N dimensional second-order differential equation into N
separate 3-dimensional equations.
However, by approximating the full electron-electron
Coulomb potential Si,j e2
/rij by a sum of terms, each depending on the
coordinates of only one electron Si,
V(ri ), one arrives at a Schrödinger equation
[-h2 /2me
Si=1  i2 - Sa
Si Za
e2 /ria + Si
V(ri)] y = E
y
i2 - Sa
Si Za
e2 /ria + Si
V(ri)] y = E
y
which is separable. That is, by assuming that
y (r1 ,
r2 , ... rN ) = f1
(r1 ) f2
(r2) ...
fN (rN),
and inserting this ansatz into the approximate Schrödinger
equation, one obtains N separate Schrödinger equations:
[-h2 /2me
 i2
- Sa Za
e2 /ria + V(ri)]
fi = Ei
fi
i2
- Sa Za
e2 /ria + V(ri)]
fi = Ei
fi
one for each of the N so-called orbitals fi
whose energies Ei are called orbital energies.
It turns out that much of the effort going on in the electronic
structure area of theoretical chemistry has to do with how one can
find the "best" effective potential V(r); that is, the
V(r), which depends only on the coordinates r of one
electron, that can best approximate the true pairwise additive
Coulomb potential experienced by an electron due to the other
electrons. The simplest and most commonly used approximation for
V(r) is the so-called Hartree-Fock (HF) potential:
V(r) fi
(r) = Sj [
Ú|fj
(r')|2 e2 /|r-r'| dr'
fi (r)
- Úfj*(r')
fj (r')
e2 /|r-r'| dr' fj
(r) ].
This potential, when acting on the orbital fi
, can be viewed as multiplying fi
by a sum of potential energy terms (which is what makes it
one-electron additive), each of which consists of two parts:
a. An average Coulomb repulsion Ú
|fj (r')|2
e2 /|r-r'| dr' between the electron in
fi with another electron whose
spatial charge distribution is given by the probability of finding
this electron at location r' if it resides in orbital
fj : |fj
(r')|2 .
b. A so-called exchange interaction between the electron in
fi with the other electron that
resides in fj..
The sum shown above runs over all of the orbitals that are
occupied in the atom or molecule.
For example, in a Carbon atom, the indices i and j run over the
two 1s orbitals, the two 2s orbitals and the two 2p orbitals that
have electrons in them (say 2px and 2py ) The
potential felt by one of the 2s orbitals is obtained by setting
fi = 2s, and summing j over
j=1s, 1s, 2s, 2s, 2px , 2py . The term
Ú |1s(r')|2
e2 /|r-r'| dr' 2s(r) gives the
average Coulomb repulsion between an electron in the 2s orbital and
one of the two 1s electrons; Ú
|2px(r')|2 e2
/|r-r'| dr' 2s(r) gives the average
repulsion between the electron in the 2px orbital and an
electron in the 2s orbital; and Ú
|2s(r')|2 e2 /|r-r'|
dr' 2s(r) describes the Coulomb repulsion between one
electron in the 2s orbital and the other electron in the 2s orbital.
The exchange interactions, which arise because electrons are Fermion
particles whose indistinguishability must be accounted for, have
analogous interpretations.
For example, Ú 1s*(r')
2s(r') e2 /|r-r'| dr'
1s(r) is the exchange interaction between an electron in
the 1s orbital and the 2s electron; Ú
2px*(r') 2s(r') e2
/|r-r'| dr' 2px(r) is the
exchange interaction between an electron in the 2px
orbital and the 2s electron; and Ú
2s*(r') 2s(r') e2
/|r-r'| dr' 2s(r) is the exchange
interaction between a 2s orbital and itself (note that this
interaction exactly cancels the corresponding Coulomb repulsion
Ú |2s(r')|2
e2 /|r-r'| dr' 2s(r), so one
electron does not repel itself in the Hartree-Fock model).
There are two primary deficiencies with the Hartree-Fock
approximation:
a. Even if the electrons were perfectly described by a
wavefunction
y (r1 ,
r2 , ... rN ) = f1
(r1 ) f2
(r2) ... fN
(rN) in which each electron occupied an
independent orbital and remained in that orbital for all time, the
true interactions among the electrons Si,j
e2 /rij are not perfectly represented by
the sum of the average interactions.
b. The electrons in a real atom or molecule do not exist in
regions of space (this is what orbitals describe) for all time; there
are times during which they must move away from the regions of space
they occupy most of the time in order to avoid collisions with other
electrons. For this reason, we say that the motions of the electrons
are correlated (i.e., where one electron is at one instant of time
depends on where the other electrons are at that same time).
Let us consider the implications of each of these two
deficiencies.
b. The imperfections in the orbital-level
picture are substantial
To examine the difference between the true Coulomb repulsion
between electrons and the Hartree-Fock potential between these same
electrons, the figure shown below is useful. In this figure, which
pertains to two 1s electrons in a Be atom, the nucleus is at the
origin, and one of the electrons is placed at a distance from the
nucleus equal to the maximum of the 1s orbital's radial probability
density (near 0.13 Å). The radial coordinate of the second is
plotted along the abscissa; this second electron is arbitrarily
constrained to lie on the line connecting the nucleus and the first
electron (along this direction, the inter-electronic interactions are
largest). On the ordinate, there are two quantities plotted: (i) the
Hartree-Fock (sometimes called the self-consistent field (SCF)
potential) Ú |1s(r')|2
e2 /|r-r'| dr', and (ii) the so-called
fluctuation potential (F), which is the true coulombic
e2/|r-r'| interaction potential minus the
SCF potential.
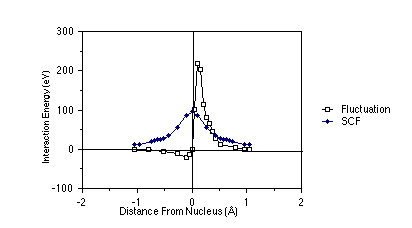
As a function of the inter-electron distance, the fluctuation
potential decays to zero more rapidly than does the SCF potential.
However, the magnitude of F is quite large and remains so over an
appreciable range of inter-electron distances. Hence, corrections to
the HF-SCF picture are quite large when measured in kcal/mole. For
example, the differences DE between the
true (state-of-the-art quantum chemical calculation) energies of
interaction among the four electrons in Be (a
and b denote the spin states of the
electrons) and the HF estimates of these interactions are given in
the table shown below in eV (1 eV = 23.06 kcal/mole).
|
Orb. Pair
|
1sa1sb
|
1sa2sa
|
1sa2sb
|
1sb2sa
|
1sb2sb
|
2sa2sb
|
|
DE in eV
|
1.126
|
0.022
|
0.058
|
0.058
|
0.022
|
1.234
|
These errors inherent to the HF model must be compared to the
total (kinetic plus potential) energies for the Be electrons. The
average value of the kinetic energy plus the Coulomb attraction to
the Be nucleus plus the HF interaction potential for one of the 2s
orbitals of Be with the three remaining electrons -15.4 eV; the
corresponding value for the 1s orbital is (negative and) of even
larger magnitude. The HF average Coulomb interaction between the two
2s orbitals of 1s22s2 Be is 5.95 eV. This data
clearly shows that corrections to the HF model represent significant
fractions of the inter-electron interaction energies (e.g., 1.234 eV
compared to 5.95- 1.234 = 4.72 eV for the two 2s electrons of Be),
and that the inter-electron interaction energies, in turn, constitute
significant fractions of the total energy of each orbital (e.g., 5.95
-1.234 eV = 4.72 eV out of -15.4 eV for a 2s orbital of Be).
The task of describing the electronic states of atoms and
molecules from first principles and in a chemically accurate manner
(± 1 kcal/mole) is clearly quite
formidable. The HF potential takes care of "most" of the interactions
among the N electrons (which interact via long-range coulomb forces
and whose dynamics requires the application of quantum physics and
permutational symmetry). However, the residual fluctuation potential
is large enough to cause significant corrections to the HF picture.
This, in turn, necessitates the use of more sophisticated and
computationally taxing techniques to reach the desired chemical
accuracy.
c. Going beyond the simplest orbital model is
sometimes essential
What about the second deficiency of the HF orbital-based model?
Electrons in atoms and molecules undergo dynamical motions in which
their coulomb repulsions cause them to "avoid" one another at every
instant of time, not only in the average-repulsion manner that the
mean-field models embody. The inclusion of instantaneous spatial
correlations among electrons is necessary to achieve a more accurate
description of atomic and molecular electronic structure.
Some idea of how large the effects of electron correlation are and
how difficult they are to treat using even the most up-to-date
quantum chemistry computer codes was given above. Another way to see
the problem is offered in the figure shown below. Here we have
displayed on the ordinate, for Helium's 1S
(1s2) state, the probability of finding an electron whose
distance from the He nucleus is 0.13Å (the peak of the 1s
orbital's density) and whose angular coordinate relative to that of
the other electron is plotted on the absissa. The He nucleus is at
the origin and the second electron also has a radial coordinate of
0.13 Å. As the relative angular coordinate varies away from
0 deg, the electrons move apart; near 0
deg, the electrons approach one another. Since both electrons have
the same spin in this state, their mutual Coulomb repulsion alone
acts to keep them apart.
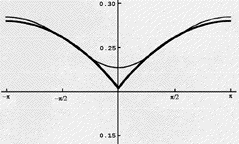
What this graph shows is that, for a highly accurate wavefunction
(one constructed using so-called Hylleraas functions that depend
explicitly on the coordinates of the two electrons as well as on
their interparticle distance coordinate) that is not of the simple
orbital product type, one finds a "cusp" in the probability density
for finding one electron in the neighborhood of another electron with
the same spin. The probability plot for the Hylleraas function is the
lower dark line in the above figure. In contrast, this same
probability density, when evaluated for an orbital-product
wavefunction (e.g., for the Hartree-Fock function) has no such cusp
because the probability density for finding one electron at r,
q, f is
independent of where the other electron is (due to the product nature
of the wavefunction). The Hartree-Fock probability, which is not even
displayed above, would thus, if plotted, be flat as a function of the
angle shown above. Finally, the graph shown above that lies above the
Hylleraas plot and that has no "sharp" cusp was extracted from a
configuration interaction wavefunction for He obtained using a rather
large correlation consistent polarized valence quadruple atomic basis
set. Even for such a sophisticated wavefunction (of the type used in
many state of the art ab initio calculations), the cusp in the
relative probability distribution is clearly not well
represented.
d. For realistic accuracy, improvements to
the orbital picture are required
Although highly accurate methods do exist for handling the
correlated motions of electrons (e.g., the Hylleraas method mentioned
above), they have not proven to be sufficiently computationally
practical to be of use on atoms and molecules containing more than a
few electrons. Hence, it is common to find other methods employed in
most chemical studies in which so-called correlated wavefunctions are
used.
By far, the most common and widely used class of such
wavefunctions involve using linear combinations of orbital product
functions (actually, one must use so-called antisymmetrized orbital
products to properly account for the fact that Fermion wavefunctions
such as those describing electrons are odd under permutations of the
electrons' labels):
Y = S
J CJ| fJ1
fJ2 fJ3
...fJ(N-!) fJN
|,
with the indices J1, J2, ..., JN labeling the spin-orbitals and
the coefficients CJ telling how much of each particular
orbital product to include. As an example, one could use
Y = C1
|1sa 1sb
| - C2 [|2pza2pzb
| - |2pxa2pxb
| -2pya2pyb
|]
as a wavefunction for the 1S state of He (the last
three orbital products are combined to produce a state that is
spherically symmetric and thus has L = 0 electronic angular momentum
just as the |1sa1sb|
state does).
Using a little algebra, and employing the fact that the orbital
products
|f1 f2
| = (2)-1/2 [ f1
f2 - f2
f1 ]
are really antisymmetric products, one can show that the above He
wavefunction can be rewritten as follows:
Y = C1/3
{|fz a
f'z b|
- |fx a
f'xb|
- |fya
f'y b|
},
where fz = 1s +
(3C2/C1)1/2 2pz and
f'z = 1s -
(3C2/C1)1/2 2pz , with
analogous definitions for fx ,
f'x , fy
, and f'y . The physical
interpretation of the three terms ({|fz
a f'z
b| , |fx
a f'x
b| , and |fy
a f'y
b| ) is that |fz
a f'z
b| describes a contribution to
Y in which one electron of a
spin resides in a region of space described by fz
while the other electron of b spin
is in a region of space described by f'z
, and analogously for |fxa
f'x b|
and |fy a
f'y b|.
Such a wavefunction thus allows the two electrons to occupy different
regions of space since each orbital f in a
pair is different from its partner f'. The
extent to which the orbital differ depends on the
C2/C1 ratio which, in turn, is governed by how
strong the mutual repulsions between the two electrons are. Such a
pair of so-called polarized orbitals is shown in the figure
below.
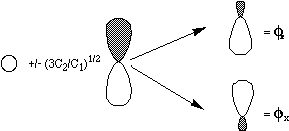
These approaches provide alternatives to the conventional tools of
quantum chemistry. The CI, MCSCF, MPPT/MBPT, and CC methods move
beyond the single-configuration picture by adding to the wave
function more configurations whose amplitudes they each determine in
their own way. This can lead to a very large number of CSFs in the
correlated wave function, and, as a result, a need for extraordinary
computer resources.
The density functional approaches are different. Here one solves a
set of orbital-level equations
[ - h2/2me  2-
SA
ZAe2/|r-RA| +
Úr(r')e2/|r-r'|dr'
2-
SA
ZAe2/|r-RA| +
Úr(r')e2/|r-r'|dr'
+ U(r)] fi
= ei fi
in which the orbitals {fi}
'feel' potentials due to the nuclear centers (having charges
ZA), Coulombic interaction with the total electron
density r(r'), and a so-called
exchange-correlation potential denoted U(r'). The
particular electronic state for which the calculation is being
performed is specified by forming a corresponding density
r(r'). Before going further in
describing how DFT calculations are carried out, let us examine the
origins underlying this theory.
The so-called Hohenberg-Kohn theorem
states that the ground-state electron density r(r)
describing an N-electron system uniquely determines the potential
V(r) in the Hamiltonian
H = Sj
{-h2/2me j2
+ V(rj) + e2/2 Skj
1/rj,k },
j2
+ V(rj) + e2/2 Skj
1/rj,k },
and, because H determines the ground-state energy and wave
function of the system, the ground-state density r(r)
determines the ground-state properties of the system. The proof of
this theorem proceeds as follows:
a. r(r) determines N because
Ú r(r) d3r =
N.
b. Assume that there are two distinct potentials (aside from an
additive constant that simply shifts the zero of total energy)
V(r) and V'(r) which, when used in H and H',
respectively, to solve for a ground state produce E0,
Y (r) and E0',
Y'(r) that have the same one-electron
density: Ú |Y|2
dr2 dr3 ... drN = r(r)=
Ú |Y'|2
dr2 dr3 ... drN .
c. If we think of Y' as trial
variational wave function for the Hamiltonian H, we know that
E0 < <Y'|H|Y'>
= <Y'|H'|Y'>
+ Ú r(r) [V(r) -
V'(r)] d3r = E0' + Ú
r(r) [V(r) - V'(r)]
d3r.
d. Similarly, taking Y as a trial
function for the H' Hamiltonian, one finds that
E0' < E0 + Ú
r(r) [V'(r) - V(r)]
d3r.
e. Adding the equations in c and d gives
E0 + E0' < E0 +
E0',
a clear contradiction.
Hence, there cannot be two distinct potentials V and V' that give
the same ground-state r(r). So, the
ground-state density r(r) uniquely
determines N and V, and thus H, and therefore Y
and E0. Furthermore, because Y
determines all properties of the ground state, then r(r),
in principle, determines all such properties. This means that even
the kinetic energy and the electron-electron interaction energy of
the ground-state are determined by r(r).
It is easy to see that Ú
r(r) V(r) d3r = V[r]
gives the average value of the electron-nuclear (plus any additional
one-electron additive potential) interaction in terms of the
ground-state density r(r), but how
are the kinetic energy T[r] and
the electron-electron interaction Vee[r]
energy expressed in terms of r?
The main difficulty with DFT is that the Hohenberg-Kohn theorem
shows that the ground-state values of T, Vee , V,
etc. are all unique functionals of the ground-state
r (i.e., that they can, in principle, be
determined once r is given), but it does
not tell us what these functional relations are.
To see how it might make sense that a property such as the kinetic
energy, whose operator
-h2 /2me  2
involves derivatives, can be related to the electron density,
consider a simple system of N non-interacting electrons moving in a
three-dimensional cubic "box" potential. The energy states of such
electrons are known to be
2
involves derivatives, can be related to the electron density,
consider a simple system of N non-interacting electrons moving in a
three-dimensional cubic "box" potential. The energy states of such
electrons are known to be
E = (h2/2meL2)
(nx2 + ny2
+nz2 ),
where L is the length of the box along the three axes, and nx
, ny , and nz are the quantum numbers
describing the state. We can view nx2 +
ny2 +nz2 = R2
as defining the squared radius of a sphere in three dimensions, and
we realize that the density of quantum states in this space is one
state per unit volume in the nx , ny , nz
space. Because nx , ny , and nz
must be positive integers, the volume covering all states with
energy less than or equal to a specified energy E =
(h2/2meL2) R2 is 1/8 the
volume of the sphere of radius R:
F(E) = 1/8 (4p/3)
R3 = (p/6)
(8meL2E/h2)3/2 .
Since there is one state per unit of such volume, F(E)
is also the number of states with energy less than or equal to E, and
is called the integrated density of states. The number of
states g(E) dE with energy between E and E+dE, the density of
states, is the derivative of F:
g(E) = dF/dE = (p/4)
(8meL2/h2)3/2
E1/2 .
If we calculate the total energy for N electrons, with the states
having energies up to the so-called Fermi energy (i.e., the
energy of the highest occupied molecular orbital HOMO) doubly
occupied, we obtain the ground-state energy:
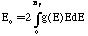 =
(8p/5)
(2me/h2)3/2 L3
EF5/2.
=
(8p/5)
(2me/h2)3/2 L3
EF5/2.
The total number of electrons N can be expressed as
N = 2 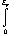 g(e)dE=
(8p/3)
(2me/h2)3/2 L3
EF3/2,
g(e)dE=
(8p/3)
(2me/h2)3/2 L3
EF3/2,
which can be solved for EF in terms of N to then
express E0 in terms of N instead of EF:
E0 = (3h2/10me)
(3/8p)2/3 L3
(N/L3)5/3 .
This gives the total energy, which is also the kinetic energy in
this case because the potential energy is zero within the "box", in
terms of the electron density r (x,y,z) =
(N/L3). It therefore may be plausible to express kinetic
energies in terms of electron densities r(r),
but it is by no means clear how to do so for "real" atoms and
molecules with electron-nuclear and electron-electron interactions
operative.
In one of the earliest DFT models, the Thomas-Fermi theory,
the kinetic energy of an atom or molecule is approximated using the
above kind of treatment on a "local" level. That is, for each volume
element in r space, one assumes the expression given above to
be valid, and then one integrates over all r to compute the
total kinetic energy:
TTF[r] =
Ú
(3h2/10me) (3/8p)2/3
[r(r)]5/3
d3r = CF Ú
[r(r)]5/3
d3r ,
where the last equality simply defines the CF constant
(which is 2.8712 in atomic units). Ignoring the correlation and
exchange contributions to the total energy, this T is combined with
the electron-nuclear V and Coulombic electron-electron potential
energies to give the Thomas-Fermi total energy:
E0,TF [r] =
CF Ú
[r(r)]5/3
d3r + Ú
V(r) r(r)
d3r + e2/2 Ú
r(r) r(r')/|r-r'|
d3r d3r',
This expression is an example of how E0 is given as a
local density functional approximation (LDA). The term local
means that the energy is given as a functional (i.e., a function of
r) which depends only on r(r)
at points in space but not on r(r)
at more than one point in space.
Unfortunately, the Thomas-Fermi energy functional does not produce
results that are of sufficiently high accuracy to be of great use in
chemistry. What is missing in this theory are a. the exchange energy
and b. the correlation energy; moreover, the kinetic energy is
treated only in the approximate manner described.
In the book by Parr and Yang, it is
shown how Dirac was able to address the exchange energy for the
'uniform electron gas' (N Coulomb interacting electrons moving
in a uniform positive background charge whose magnitude balances the
charge of the N electrons). If the exact expression for the exchange
energy of the uniform electron gas is applied on a local level, one
obtains the commonly used Dirac local density approximation to the
exchange energy:
Eex,Dirac[r]
= - Cx Ú
[r(r)]4/3
d3r,
with Cx = (3/4) (3/p)1/3
= 0.7386 in atomic units. Adding this exchange energy to the
Thomas-Fermi total energy E0,TF [r]
gives the so-called Thomas-Fermi-Dirac (TFD) energy functional.
|

|
|

|
|
Professor Bob Parr
|
|
Professor Weitao Yang
|
Because electron densities vary rather strongly spatially near the
nuclei, corrections to the above approximations to T[r]
and Eex.Dirac are needed. One of the more commonly used
so-called gradient-corrected approximations is that invented
by Becke, and referred to as the
Becke88 exchange functional:
Eex(Becke88) =
Eex,Dirac[r]
-g Ú
x2 r4/3
(1+6 g x
sinh-1(x))-1 dr,
where x =r-4/3
| r|,
and g is a parameter chosen so that the
above exchange energy can best reproduce the known exchange energies
of specific electronic states of the inert gas atoms (Becke finds
g to equal 0.0042). A common gradient
correction to the earlier T[r] is
called the Weizsacker correction and is given by
r|,
and g is a parameter chosen so that the
above exchange energy can best reproduce the known exchange energies
of specific electronic states of the inert gas atoms (Becke finds
g to equal 0.0042). A common gradient
correction to the earlier T[r] is
called the Weizsacker correction and is given by
dTWeizsacker =
(1/72)(h/me) Ú
| r(r)|2/r(r)
dr.
r(r)|2/r(r)
dr.
Although the above discussion suggests how one might compute the
ground-state energy once the ground-state density r(r)
is given, one still needs to know how to obtain r.
Kohn and Sham (KS) introduced a set of so-called KS orbitals obeying
the following equation:
{-1/2 2
+ V(r) + e2/2 Ú
r(r')/|r-r'|
dr' + Uxc(r) }fj
= ej fj
,
2
+ V(r) + e2/2 Ú
r(r')/|r-r'|
dr' + Uxc(r) }fj
= ej fj
,
where the so-called exchange-correlation potential Uxc
(r) = dExc[r]/dr(r)
could be obtained by functional differentiation if the
exchange-correlation energy functional
Exc[r] were known. KS
also showed that the KS orbitals {fj}
could be used to compute the density r by
simply adding up the orbital densities multiplied by orbital
occupancies nj :
r(r) = Sj
nj |fj(r)|2.
(here nj =0,1, or 2 is the occupation number of the orbital
fj in the state being studied)
and that the kinetic energy should be calculated as
T = Sj
nj <fj(r)|-1/2
 2
|fj(r)>.
2
|fj(r)>.
The same investigations of the idealized 'uniform electron gas'
that identified the Dirac exchange functional, found that the
correlation energy (per electron) could also be written exactly as a
function of the electron density r
of the system, but only in two limiting cases- the high-density limit
(large r) and the low-density limit. There
still exists no exact expression for the correlation energy even for
the uniform electron gas that is valid at arbitrary values of
r. Therefore, much work has been devoted
to creating efficient and accurate interpolation formulas connecting
the low- and high- density uniform electron gas expressions (see
Appendix E in the Parr and Wang book for further details). One such
expression is
EC[r] =
Ú r(r) ec(r)
dr,
where
ec(r)
= A/2{ln(x/X) + 2b/Q tan-1(Q/(2x+b))
-bx0/X0
[ln((x-x0)2/X)
+2(b+2x0)/Q tan-1(Q/(2x+b))]
is the correlation energy per electron. Here x =
rs1/2 , X=x2 +bx+c, X0
=x02 +bx0+c and Q=(4c -
b2)1/2, A = 0.0621814, x0=
-0.409286, b = 13.0720, and c = 42.7198. The parameter rs
is how the density r enters since
4/3 prs3 is equal to
1/r; that is, rs is the radius
of a sphere whose volume is the effective volume occupied by one
electron. A reasonable approximation to the full
Exc[r] would contain
the Dirac (and perhaps gradient corrected) exchange functional plus
the above EC[r], but
there are many alternative approximations to the exchange-correlation
energy functional. Currently, many workers are doing their best to
"cook up" functionals for the correlation and exchange energies, but
no one has yet invented functionals that are so reliable that most
workers agree to use them.
To summarize, in implementing any DFT, one usually proceeds as
follows:
1. An atomic orbital basis is chosen in terms of which the KS
orbitals are to be expanded.
2. Some initial guess is made for the LCAO-KS expansion
coefficients Cj,a: fj
= Sa Cj,a
ca.
3. The density is computed as r(r)
= Sj nj
|fj(r)|2
. Often, r(r) is expanded in an
atomic orbital basis, which need not be the same as the basis used
for the fj, and the expansion
coefficients of r are computed in terms of
those of the fj . It is also
common to use an atomic orbital basis to expand r1/3(r)
which, together with r, is needed to
evaluate the exchange-correlation functional's contribution to
E0.
4. The current iteration's density is used in the KS equations to
determine the Hamiltonian
{-1/2  2
+ V(r) + e2/2 Ú
r(r')/|r-r'|
dr' + Uxc(r) }whose "new" eigenfunctions
{fj} and eigenvalues
{ej} are found by solving the
KS equations.
2
+ V(r) + e2/2 Ú
r(r')/|r-r'|
dr' + Uxc(r) }whose "new" eigenfunctions
{fj} and eigenvalues
{ej} are found by solving the
KS equations.
5. These new fj are used to
compute a new density, which, in turn, is used to solve a new set of
KS equations. This process is continued until convergence is reached
(i.e., until the fj used to
determine the current iteration's r are
the same fj that arise as
solutions on the next iteration.
6. Once the converged r(r) is
determined, the energy can be computed using the earlier
expression
E [r] = Sj
nj <fj(r)|-1/2
 2
|fj(r)>+
Ú V(r)
r(r) dr + e2/2
Ú r(r)r(r')/|r-r'|dr
dr'+ Exc[r].
2
|fj(r)>+
Ú V(r)
r(r) dr + e2/2
Ú r(r)r(r')/|r-r'|dr
dr'+ Exc[r].
In closing this section, it should once again be emphasized that
this area is currently undergoing explosive growth and much scrutiny.
As a result, it is nearly certain that many of the specific
functionals discussed above will be replaced in the near future by
improved and more rigorously justified versions. It is also likely
that extensions of DFT to excited states (many workers are actively
pursuing this) will be placed on more solid ground and made
applicable to molecular systems. Because the computational effort
involved in these approaches scales much less strongly with basis set
size than for conventional (SCF, MCSCF, CI, etc.) methods, density
functional methods offer great promise and are likely to contribute
much to quantum chemistry in the next decade.
There is a nice DFT web
site established by the Arias
research group at Cornell devoted to a DFT project involving
highly efficient computer implementation within object-oriented
programming.
f. Efficient and widely distributed computer
programs exist for carrying out electronic structure calculations
The development of electronic structure theory has been ongoing
since the 1940s. At first, only a few scientists had access to
computers, and they began to develop numerical methods for solving
the requisite equations (e.g., the Hartree-Fock equations for
orbitals and orbital energies, the configuration interaction
equations for electronic state energies and wavefunctions). By the
late 1960s, several research groups had developed reasonably
efficient computer codes (written primarily in Fortran with selected
subroutines that needed to run especially efficiently in machine
language), and the explosive expansion of this discipline was
underway. By the 1980s and through the 1990s, these electronic
structure programs began to be used by practicing "bench chemists"
both because they became easier to use and because their efficiency
and the computers' speed grew (and cost dropped) to the point at
which modest to large molecules could be studied at reasonable cost
and effort.
Even with much faster computers, there remain severe bottlenecks
to extending ab initio quantum chemistry tools to larger and larger
molecules (and to extended systems such as polymers, solids, and
surfaces). Two of the most difficult issues involve the two-electron
integrals
(ci cj
|1/r1,2| ck
cl ). Nearly all correlated
electronic structure methods express the electronic energy E (as well
as its gradient and second derivative or Hessian) in terms of
integrals taken over the molecular orbitals, not the basis atomic
orbitals. This usually then requires that the integrals be first
evaluated in terms of the basis orbitals and subsequently transformed
from the basis orbital to the molecular orbital representation using
the LCAO-MO expansion fj =
Sa Cj,a ca.
For example, one such step in the transformation involves
computing
Sa Cj,a
(ca cj
|1/r1,2| ck
cl ) = (fi
cj |1/r1,2|
ck cl
).
Four such one-index transformations must performed to eventually
obtain the (fi fj
|1/r1,2| fk
fl ) integrals. Given a set of
M basis orbitals, there are ca. M4/8 integrals
(ca cj
|1/r1,2| ck
cl ). Each one-index
transformation step requires ca. M5 calculations (i.e., to
form the sum of products such as Sa
Cj,a (ca
cj |1/r1,2|
ck cl
). Hence the task of forming these integrals over the molecular
orbitals scales as the fifth power of M.
The research group of Professor Martin
Head-Gordon has been attacking two aspects of the above integral
bottleneck.

Professror Martin Head-Gordon
First, his group has been deriving and implementing in a very
efficient manner expressions for the electronic energy (and its
gradient with respect to nuclear positions ) that are not written in
terms of integrals over the molecular orbitals but in terms of
integrals over the basis atomic orbitals. This allows them to produce
what are called "direct" procedures for evaluating energies and
gradients. The advantages of such direct methods are (1) that one
does not have to go through the M5 integral transformation
process, and (2) that one does not have to first compute all of the
atomic-orbital integrals (ci
cj |1/r1,2|
ck cl
). Instead, one can compute groups of these integrals (ci
cj |1/r1,2|
ck cl
) (e.g., as many as one can retain within the fast main memory of the
computer), calculate the contributions made by these integrals to the
energy or gradient, and then delete this group of integrals and
proceed to compute (and use) another group of such integrals. This
allows one to handle larger basis sets than when one has to first
obtain all of the integrals and store them (e.g., on disk). The
second major advance that the Head-Gordon group has fostered is
developing clever and efficient new tools for computing the
atomic-orbital-level two-electron integrals (ci
cj |1/r1,2|
ck cl
), especially when the product functions ci
(1) cj (1) and ck
(2) cl (2) invlove functions
that are distant from one another. When there is good reason to view
these products as residing in different regions of space (e.g., when
the constitutent atomic orbitals are centered on atoms in different
parts of a large molecule), so-called multipole expansion methods
(and other tools) can be used to approximate the two-electron
integrals (ci cj
|1/r1,2| ck
cl ). In this way, the
Head-Gordon group has been able to (a) calculate integrals in which
all of the basis orbitals reside on the same or very nearby atoms in
conventional (highly efficient) ways, (b) approximate (very rapidly
and in a numerically reliable multipolar manner) the integrals where
the charge densities are somewhat distant yet still significant, and
(c) ignore (to controlled tolerances) integrals for product densities
that are even more distant. This has allowed them to obtain integral
evaluation and energy-computation schemes that display nearly linear
scaling with the number of atoms (and thus basis orbitals) in the
system. It is only through such efforts that there is any hope of
extending ab initio electronic structure mehtods to large molecules
and extended systems.
The Head-Gordon group has also been expanding the horizons of the
very powerful coupled-cluster method for treating electron
correlation at a high level, especially by introducing so-called
local-methods for handling interactions among electrons. In
particular, by making clever defintions of localized occupied and
virtual orbitals, they have been able to develop new methods whose
computational effort promises to scale more practically with the
number of electrons (i.e., the molecule size) than do conventional
coupled cluster methods. Combining their advances in coupled-cluster
theory with their breakthroughs in handling electron-electron
interactions, has lead to a large body of important new work from
this outstanding group.
At present, more electronic structure calculations are performed
by non-theorists than by practicing theoretical chemists. This is
largely due to the proliferation of widely used computer programs.
This does not mean that all that needs to be done in electronic
structure theory is done. The rates at which improvements are being
made in the numerical algorithms used to solve the problems as well
as at which new models are being created remain as high as ever. For
example, Professor Rich
Friesner has developed and Professor
Emily Carter has implemented for correlated methods a highly
efficient way to replace the list of two-electron integrals
(fi fj
|1/r1,2| fk
fl ), which number
N4 , where N is the number of atomic orbital basis
functions, by a much smaller list (fi
fj |l)
from which the original integrals can be rewritten as: (fi
fj |1/r1,2|
fk fl
) = Sg (fi
(g)fj (g))
Ú dr fk(r)
fl (r)/|r-g|
.

|
|
|
|
Professor Rich Friesner
|
|
Professor Emily Carter
|
This tool, which they call pseudospectral methods, promises to
reduce the CPU, memory, and disk storage requirements for many
electronic structure calculations, thus permitting their applications
to much larger molecular systems.
In addition to ongoing developments in the underlying theory and
computer implementation, the range of phenomena and the kinds of
physical properties that one needs electronic structure theory to
address is growing rapidly. Professor Gustavo
Scuseria has been especially active in developing new methods for
treating very large molecules, in particular, methods whose computer
requirements scale linearaly (or nearly so) with molecular size.
In addition, a great deal of progress has been made in
constructing sequences of atomic orbital basis sets whose use allows
one to extrapolate to essentially complete-basis quality results.
Thom Dunning has, more than anyone else, been responsible for
progress in this area.

|
|

|
|
Professor Gustavo Scuseria
|
|
Dr. Thom Dunning
|
There are a variety of tools that aim to compute differences
betweeen state energies (e.g., electron affinities, ionization
potentials, and excitation energies) directly. Several workers who
have been instrumental in developing these methods include those
shown below.


Professors Lorenz
Cederbaum (l), University of Heidelberg, Professor Jan
Linderberg (r), Aarhus University, and Professor Yngve
Ohrn (below), University of Florida.

Also, Professor Howard Taylor, University of Southern California
(below) contributed much to these developments as well as to methods
for treating metastable electronic states.

In more recent years, the author, Professor J.
V. Ortiz (below, l), Kansas State University, Professor P.
Jørgensen (below, r), and Profesor J.
Oddershede (bottom) have continued to develop these and related
methods.



In addition to the many practicing quantum chemists introduced
above, I show below photos of several others whose research and
educational efforts will be of interest to students reading this web
site.

|
|

|
- Professor Krishnan
Balusubramanian
- University of California, Davis
|
|
- Professor Jerzy Cioslowski
- Florida State University
|

Professor Marcel
Nooijen, University of Waterloo
In addition to Prof. Balusubramanian, another expert on the
effects of relativity on atomic and molecular properties is Prof.
Pekka Pyykko of
Helsinki University (below). This dynamic scholar always give a
wonderful talk on how relativity contributes to many properties of
matter in nature.

Most people know that the study of transition metal containing
systems is especially difficult because of the near-degeneracy of the
ns and (n-1) d orbitals and the role of relativistic effects in the
heavier elements. Prof. Gernot Frenking of the University of Marburg,
shown below, has devoted a great deal of effort to understanding such
systems. His group has also developed a powerful and useful means of
decomposing the bonding interactions among atoms into various
physical contributions.

Professor Gernot
Frenking
Professor Piotr Piecuch, Michigan State University, has been
involved in extending the coupled-cluster method to allow one to use
multiconfigurational reference wave functions, which is very
important when one wishes to describe diradicals and bond-breaking
and bond-forming proceses. He and his co-workers have forumlated what
they call a renormalized coupled-cluster method that can accurately
describe bond breaking and excited electronic surfaces at a
computational cost similar to that of a single-configuration
reference calculation. They have also been looking into using
explicitly correlated two-electron exponential cluster expansions of
the N-electron wave function to see to what extent one can capture
most (if not all) of the electron-electron correlations within such a
compact framework.

Professor Piotr
Piecuch (upper left) with his research group at Michigan State
Univesity

Professor Nicholas
Handy (above), Cambridge University, has made numerous
contributions to electronic structure theory, to the theory of
molecular spectroscopy, and to the rapidly expanding field of density
functional theory.

Professor Jose
Ramon Alvarez Collado (above) has made several contributions to
Hartree-Fock and configuration interaction theory as well as to the
treatment of vibtrational Hamiltonia and vibrational motions of
molecules. He recently has shown how to handle large clusters or
solid materials that contain a very large number of unpaired
electrons.

Professor Bjørn
Roos, Lund University, Sweden has been one of his nation's
leading quantum chemists for many years, has developed one of the
most powerful and widely used quantum chemistry codes, and has
organized many schools on quantum chemistry.
Professor Jerzy
Leszczynski at Jackson State University has established a very
strong program in quantum chemistry and has hosted many very
important conferences as well as "schools".

Professor Kimihiko
Hirao's group in Tokyo has made many important contributions to
the development and applications of modern quantum chemistry tools,
especially those involving multi-configurational wave functions.

There exists an approach to solving the Schrödinger equation
that has proven to be extremely accurate and is based on viewing the
time-dependent Schrödinger equaiton as a diffusion equation with
its time variable defined as imaginary. The idea then is to propagate
an "initial" wavefunction (chosen to possess the proper permutational
and symmetry properties of the desired solution) forward in time with
the diffusion equation (having a source and sink term arising from
the electron-nuclear and electron-electron Coulomb potentials). It
can be shown that such a propogated wavefunction will converge to the
lowest energy state that has the symmetry and nodal behavior of the
trial wavefunction. The people who have done the most to propose,
implement, and improve such so-called Diffusion Monte-Carlo type
procedures include:
Professor James
Anderson of Penn State University

Professor Bill
Lester, University of California, Berkeley

Professor Jules
Moskowitz of New York University

and Professor David
Ceperley of the University of Illinois

Professor Greg Gellene, Texas Tech, has pioneered the study of
Rydberg species and of concerted reactions of small molecules and
molcular compexes.

Greg Gellene
Professor Anna
Krylov, University of Southern California, has been developing
new electronic structure methods aimed at particularly difficult
classes of compounds where multiconfigurational wave functions are
essential. These include diradical and triradical species.

Professor Debbie
Evans, University of New Mexico, has been working on electron
transport and other quantum dynamics in branched macromolecules and
other condensed phase systems.

Professor Angela Wilson, University of North Texas has done a lot
to calibrate basis sets so we know to what extent we can trust them
in various kinds of electronic structure calculations.

Prof. Angela
Wilson
Professor Thomas Cundari, University of North Texas, is very
active in using electronic structure methods to study inorganic and
organometallic species.

Prof. Thomas
Cundari (red shirt).
Professor Wes Borden recently joined the University of North
Texas as Welch Professor. He has a long and distinguished record of
applying quantum chemistry to important problems in organic
chemistry.

Prof. Wes
Borden
Professor Ludwik
Adamowicz (below) of the University of Arizona has done a lot of
work on molecular anions, especially
dipole-bound anions involving bio-molecules. He has also done much
work on multi-reference coupled cluster methods,
method for generating non-adiabatic multiparticle wave functions,
and for calculating rovibrational states of polyatomic molecules.

Professor Kwang
Kim, is using a variety of theoretical methods to study
functional materials with the support of Creative Research
Initiativ,
Ministry of Science and Technology of Korea. His laboratory has
three subdivisions: (1) the quantum theoretical chemistry
group, (2) a theoretical condensed matter physics group, and (3)a
synthesis and property measurement group.

Indiana University has had a long tradition of excellence in
theoretical chemistry. Currently, its chemistry faculty include Prof.
Peter Ortoleva, Prof. Krishnan Raghavachari, and Prof. Srinivasan
Iyengar who are shown below.

Professor Peter
Ortoleva who works on pattern formations within biological
systems as well as in geology.

Professor Krishnan
Raghavachari who has made numerous advances in quantum chemical
methodologies and in the study of small to moderate size clusters of
main group atoms.

Prof.
Srinivasan
Iyengar who developed the atom-centered density matrix
propogation method for combining electronic structure and
collision/reaction dynamics and is applying this to a wide variety of
problems.
At Notre Dame University, there are also several faculty
specializing in theory. They include

Prof. Eli
Barkai who studies single-molecule spectroscopy and fractional
kinetics.

Prof. Dan
Gezelter who studies condensed-phase molecular dynamics, and

Prof. Dan
Chipman who is interested in solvation effects, electronic
structure methods developments and free radicals.
Several recent new faculty hires have been made in extremely good
chemistry departments including those shown below. We need to be
looking out for many good new developments from these people.

Prof. Garnet
Chan, Cornell University, says the following about his group's
work:
Our work is in the area of the electronic structure and dynamics
of complex processes. We engage in developing new and more powerful
theoretical techniques which enable us to describe strong electronic
correlation problems.
Of particular theoretical interest are the construction of fast
(polynomial) algorithms to solve the quantum many-particle problem,
and the treatment of correlation in time-dependent processes.
A key feature of our theoretical approach is the use of modern
renormalization group and multi-scale ideas. These enable us to
extend the range of simulation from the simple to the complex, and
from the small to the very large.
Some current phenomena under study include:
(i) Energy and electron transfer in conjugated polymers:
specifically photosynthetic carotenoids, optoelectronic polymers, and
carbon nanotubes,
(ii) Spin couplings in multiple-transition metal systems,
including iron-sulfur proteins and molecular magnets.
(iii) Lattice models of high Tc superconductors.

Profesor Phillip
Geissler, University of California, Berkeley

Professor Troy
van Voorhis, MIT, says the following about his group's work:
The Van Voorhis group develops new methods that make reliable
predictions about real systems for which existing techniques are
inadequate. At present, our ideas center around the following major
themes: the value of explicitly time-dependent theories, the
importance of electron correlation and the proper treatment of
delicate effects such as van der Waals forces and magnetic
interactions.
Electronic Structure of Molecular Magnetism
Molecular magnetism is currently a ``hot'' area in chemical
physics because of the technological promise of colossal
magneto-resistant materials compounds and super-paramagnetic
molecules. We are interested in developing a better fundamental
understanding of magnetism that will allow us to predict the behavior
of systems like these in an ab initio way. For example, one should be
able to extract the Heisenberg exchange parameters (even for
challenging oxo-bridged transition metal compounds) by simulating the
response of the system to localized magnetic fields. We are also
interested in extending the commonly used Heisenberg Hamiltonian to
include spin orbit interactions in a local manner. This would be
useful, for example, if one is interested in assembling a large
molecule out of smaller building blocks - by knowing the preferred
axis of each fragment one could potentially extract the magnetic axis
and anisotropy of the larger compound.
Modeling Real-Time Electron Dynamics
Ab initio methods tend to focus the lion's share of attention on
the description of electronic structure. However, there are a variety
of systems where a focus on the electron dynamics is extremely
fruitful. On the one hand, there are systems where it is the motion
of the electrons that is interesting. This is true, for example, in
conducting organic polymers and crystals - where it is charge
migration that leads conductivity - and in photosynthetic and
photovoltaic systems - where excited state energy transfer determines
the efficiency. Also, in a very deep way, dynamic simulations can
offer improved pictures of static phenomena. Here, our attention is
focused on the fluctuation-dissipation theorem, an exact relation
between the static correlation function and the time-dependent
response of the system, and on semiclassical techniques, which
provide a simple ansatz for approximating quantum results using
essentially classical information.

Prof. Aaron
Dinner, Univ. of Chicago

Prof. Misha
Ovchinnikov, Univ. of Rochester

Prof.
David Mazziotti, Univ. of Chicago
Web page links to many of the more widely used programs offer
convenient access:
Pacific Northwest Labs is developing a suite of programs called
NWChem
The MacroModel
program
The Gaussian suite of
programs
The GAMESS
program
The HyperChem programs of
Hypercube, Inc.
The CAChe software
packages from Fujitsu
The Spartan sofware package
of Wavefunction, Inc.
The MOPAC program of
CambridgeSoft
The Amber
program of Prof. Peter Kollman, University of California, San
Francisco
The CHARMm
program
The programs of Accelrys,
Inc.
The COLUMBUS
program
The CADPAC
program of Dr. Roger Amos
The programs of Wavefunction,
Inc.
The ACES II program of
Prof. Rod Bartlett.
The MOLCAS
program of Prof. Bjorn Roos.
The MOLPRO quantum
chemistry package of Profs. Werner and Knowles
The Vienna Ab Initio Simulations Package (VASP)
A nice compendium of various softwares is given in the Appendix of
Reviews in Lipkowitz K B and Boyd D B (Eds) 1996 Computational
Chemistry (New York, NY: VCH Publications) Vol 7
I hope the discussion I have offered has made it clear that there
is every reason to believe that this sub-discipline of theoretical
chemistry will continue to blossom for many years to come. Clearly,
electronic structure theory provides a wealth of information about
molecular structure and molecular properties. It does not, however,
give us all the information we need to characterize a molecule's full
motions. What is missing primarily is a description of the movements
of the nuclei (or, equivalently, the bond lengths and angles and
intermolecular coordinates), whose study lies within the realm of the
next sub-discipline of theoretical chemistry to be discussed.
B. Molecular and
chemical dynamics describes the motions of the atoms within the
molecule and the surrounding solvent
The collisions among molecules and resulting energy transfers
among translational, vibrational, rotational, and electronic modes,
as well as chemical reactions that occur intramolecularly or in
bi-molecular encounters lie within the realm of molecular and
chemical dynamics theory. The vibrational and rotational motions that
a molecule's nuclei undergo on any one of the potential energy
surfaces EkQ) is also a subject for molecular dynamics and
provides a logical bridge to the subject of molecular
vibration-rotation spectroscopy.
1. Classical Newtonian Dynamics Can Often Be
Used
For any particular molecule with its electrons occupying one of
its particular electronic states, the atomic centers (i.e., the N
nuclei) undergo translational, rotational, and vibrational movements.
The translational and rotational motions do not experience any forces
and are thus "free motions" unless (1) surrounding solvent or lattice
species are present or (2) an external electric or magnetic field is
applied. Either of the latter influences will cause the translations
and rotations to experience potential energies that depend on the
location of the molecule's center of mass and the molecule's
orientation in space, respectively.
In contrast, the vibrational coordinates of a molecule experience
forces that result from the dependence of the electronic state energy
Ek on the internal coordinates
Fi = - dEk({Q})/dQi.
By expressing the kinetic energy T for internal vibrational
motions and the corresponding potential energy V= Ek({Q})
in terms of 3N-6 internal coordinates {Qk}, classical
equations of motion based on the so-called Lagrangian L = T - V:
d/dt d[T-V]/d i
= d[T-V]/dQi
i
= d[T-V]/dQi
can be developed. If surrounding solvent species or external
fields are present, equations of motion can also be developed for the
three center of mass coordinates R and the three orientational
coordinates W . To do so one must
express the molecule-solvent intermolecular potential energy in terms
of R and W, and the
translational and orientational kinetic energies must also be written
in terms of the time rates of change of R and W.
The equations of motion discussed above are classical. Most
molecular dynamics theory and simulations are performed in this
manner. When light atoms such as H, D, or He appear, it is often
essential to treat the equations of motion that describe their
motions (vibrations as well as translations and rotations in the
presence of solvent or lattice surroundings) using the
Schrödinger equation instead. This is a much more difficult
task.
a. A collision between an atom and a
diatomic molecule
Let us consider an example to illustrate the classical and quantum
treatments of dynamics. In particular, consider the collision of an
atom A with a diatomic molecule BC with all three atoms constrained
to lie in a plane.
I. The coordinates in which the kinetic
energy has no cross terms
Here the three atoms have a total of 2N = 6 coordinates because
they are constrained to lie in the X,Y plane. The center of mass of
the three atoms
x = (mA xA + mB xB
+ mC xC )/M
y = (mA yA + mB yB
+ mC yC )/M
requires two coordinates to specify, which leaves 2N-2 = 4
coordinates to describe the internal and overall orientational
arrangement of the three atoms. It is common (the reason will be
explained below) in such triatomic systems to choose the following
specific set of internal coordinates:
1. r, the distance between two of the atoms (usually the two that
are bound in the A + BC collision);
2. R, the distance of the third atom (A) from the center of mass
of the first two atoms (BC);
3. a and b ,
two angles between the r and R vectors and the
laboratory-fixed X axis, respectively.
II. The Hamiltonian or total energy
In terms of these coordinates, the total energy (i.e., the
Hamiltonian) can be expressed as follows:
H = 1/2 m' 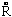 2
+ 1/2 m
2
+ 1/2 m  2
+ 1/2 m'R2
2
+ 1/2 m'R2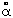 2
+ 1/.2 m r2
2
+ 1/.2 m r2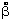 2
2
+ 1/2 M (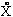 2
+
2
+ 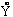 2
) + V.
2
) + V.
Here, m is the reduced mass of the BC
molecule (m =
mBmC/(mB +mc )) M is the
mass of the entire molecule M = mA + mB +
mC , and m' is the reduced mass of A relative to BC (m' =
mAmBC/(mA +mBC )). The
potential energy V is a function of R, r, and q
= a + b the
angle between the r and R vectors.
III. The conjugate momenta
To eventually make a connection to the quantum mechanical
Hamiltonian, it is necessary to rewrite the above H in terms of the
coordinates and their so-called conjugate momenta. For any coordinate
Q, the conjugate momentum PQ is defined by
PQ =  L/
L/
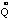 .
.
For example,
PR = m' ,
,
Pr = m  ,
,
Pa = m'
R2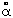 ,
,
Pb = m
r2
allow H to be rewritten as
H = PR2/2m' + Pr2
/2m + Pa2
/2m'R2 + Pb2
/2mr2 +
(PX2 + PY2 )/2M +V.
Because the potential V contains no dependence on X or Y, the
center of mass motion (i.e., the kinetic energy (PX 2
+ PY 2 )/2M) will time evolve in a
straight-line trajectory with no change in its energy. As such, it
can be removed from further consideration.
The total angular momentum of the three atoms about the Z- axis
can be expressed in terms of the four remaining coordinates as
follows:
LZ = m' R2  -
m r2
-
m r2 = Pa -
Pb .
= Pa -
Pb .
Since this total angular momentum is a conserved quantity (i.e.,
for each trajectory, the value of LZ remains unchanged
throughout the trajectory), one can substitute this expression for
Pa and rewrite H in
terms of only three coordinates and their momenta:
H = PR2 /2m' + pr2
/2m + (LZ
-Pb )2
/2m'R2 + Pb2
/2mr2 +V.
Notice that Pb is
the angular momentum of the BC molecule (Pb
= m r2 db/dt).
IV. The equations of motion
From this Hamiltonian (or the Lagrangian L = T - V), one can
obtain, using d/dt d[T-V]/d i
= d[T-V]/dQi , the equations of motion for the
three coordinates and three momenta:
i
= d[T-V]/dQi , the equations of motion for the
three coordinates and three momenta:
dPR /dt =  L/
L/ R
= -
R
= - V/
V/ R
- (LZ -Pb
)2 /m'R3 ,
R
- (LZ -Pb
)2 /m'R3 ,
dPr /dt = - V/
V/ r
- Pb2
/mr3 ,
r
- Pb2
/mr3 ,
dPb /dt =
- V/
V/ b
= -
b
= - V/
V/ q
,
q
,
dR/dt = PR /m',
dr/dt = Pr /m ,
db/dt = Pb
/mr2 .
V. The initial conditions
These six classical equations of motion that describe the time
evolution of r, R, b, PR ,
pr , and Pb can then
be solved numerically as discussed earlier. The choice of initial
values of the coordinates and momenta will depend on the conditions
in the A + BC collision that one wishes to simulate. For example, R
will be chosen as very large, and PR will be negative
(reflecting inward rather than outward relative motion) and with a
magnitude determined by the energy of the collision
PR2 /2m' = Ecoll.. If the
diatomic BC is initially in a particular vibrational state, say v,
the coordinate r will be chosen from a distribution of values given
as the square of the v-state's vibrational wavefunction |yv
(r)|2 . The value of pr can then be
determined within a sign from the energy ev
of the v state: pr2 /2m
+ VBC = ev , where
VBC is the BC molecule's potential energy as a function of
r. Finally, the angle b can be selected
from a random distribution within 0<b<2p,
and Pb would be
assigned a value determined by the rotational state of the BC
molecule at the start of the collision.
VI. Computer time requirements
The solution of the above six coupled first order differential
equations may seem like it presents a daunting task. This is,
however, not at all the case given the speed of modern computers. For
example, to propagate these six equations using time steps of
dt = 10-15 sec (one must employ
a time step that is smaller than the period of the fastest motion- in
this case, probably the B-C vibrational period which can be ca.
10-14 sec) for a total time interval of one nanosecond
Dt = 10-9 sec, would require of
the order of 106 applications of the above six equations.
If, for example, the evaluation of the forces or potential
derivatives appearing in these equations requires approximately 100
floating point operations (FPO), this 1 nanosecond trajectory would
require about 108 FPOs. On a 100 Mflop (Mflop means
million floating point operations per sec) desktop workstation, this
trajectory would require only one second to run!
You might wonder about how long trajectories on much larger
molecules would run. The number of coordinates and momenta involved
in any classical dynamics simulations is 3N-6. The evaluation of the
force on any one atom due to its interactions with other atoms
typically requires computer time proportional to the number of other
atoms (since potentials and thus forces are often pairwise additive).
In such cases, the number of FPOs would be approximately:
#FPO = 100 x (Dt/dt)
x ((3N-6)/3) x (3N-7)/2,
where the (3N-6)/3 factor scales the number of coordinates and
momenta from 3 in the above example to the number for a general
molecule containing N atoms, and (3N-9)/2 scales the number of
"other" coordinates that enter into the force calculation for any
given coordinate. Thus, we expect #FPO to vary as
#FPO = 100 x (Dt/dt)
x 3N2 /2
for large N. Thus a trajectory run for 1 ns with time steps of
10-15 sec on a large bio-molecule containing 1000 atoms
would require approximately
#FPO = 1.5 x 1014
operations. Even with a 100 Mflop computer, this trajectory would
run for 1.5 x106 sec (or ca. 17 days!).
For such large-molecule simulations, which are routinely carried
out these days, it is most common to "freeze" the movement of the
high frequency coordinates (e.g., the C-H bond stretching motions in
a large bio-molecule), so that longer time steps can be taken (e.g.,
this may allow one to take dt = 10-14
sec or longer). It is also common to ignore the forces produced
on any given atom by those atoms that are far removed from the given
atom. In this way, one can obtain a simulation whose FPO requirements
do not scale as N2 but as NxN', where N' is the number of
atoms close enough to produce significant forces. By making such
approximations, classical trajectory simulations on molecules (or
molecules with solvent species also present) containing 1000 or more
moving atoms can be carried out in a matter of a few minutes per
trajectory.
b. Monitoring the outcome of a classical
trajectory
Let us consider a case in which the collision A + BC is followed
from its initial conditions through a time at which the A atom has
struck the BC molecule and been scattered so A and BC are now
traveling away from one another. In such a situation, we speak of a
non-reactive collision.
Alternatively, the A + BC collision may result in formation of AB
+ C, which, of course, corresponds to a chemically reactive
collision. In this case, to follow the trajectory toward its ultimate
conclusion, it is common to employ a different set of internal
coordinates than were used in the early part of the collision. In
particular, one changes to two new distance and two new angular
coordinates as shown below.
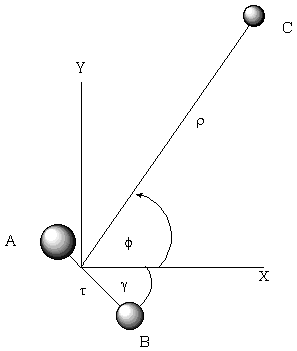
These coordinates are analogous to those used to describe A + BC
and are: r the distance from C to the
center of mass of AB, t the AB
internuclear distance, and two angles (g
and f) between the x- axis and
t and r,
respectively.
So, as the classical Newton equations are solved in a step-by-step
manner, eventually one changes from solving the equations for the
time evolution of R, r, a, and
b and their momenta to solving the
corresponding equations for r, t, f, and
g and their conjugate momenta. Then, once
the C atom is far enough away (and still moving outward) to declare
the collision ended, one can interrogate its outcome. In particular,
one can examine the vibrational and/or rotational energy content of
the product (BC in the non-reactive case; AB in the reactive case)
diatomic molecule, and one can compute the relative kinetic energy
(e.g., 1/2 m' (dr/dt)2 in the
reactive case) with which the product fragments are moving away from
one another. It is through such interrogation that one extracts
information from classical trajectory simulations.
Professor Barbara Garrison, Penn State University, has exploited
such classical trajectory simulations to study reactions and energy
transfer processes taking place when an atom, ion, or molecule
impacts a surface that may undergo ablation as a result of the
impact.

Professor Barbara
Garrison, Penn State University.
2. Sometimes Quantum Dynamics are Required
Let us now consider the above A + BC collision dynamics simulation
but from the point of view of the quantum mechanical Schrödinger
equation. This is a much more difficult problem to treat. Why?
Because instead of having to solve six coupled first order
differential equations subject to specified initial conditions, one
must solve one four-dimensional partial differential equation:
Hy = E y,
where
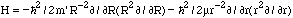
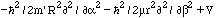
or one must propagate in time
y (R,r,a,b;t)
= exp[-i Ht/h ] y(R,r,a,b;t=0)
to find y at time t, given initial
conditions for y at t=0.
a. What needs to be done to apply the
Schrödinger equation?
I. An initial wavefunction must be
given
Specifying an initial wavefunction y(R,r,a,b;t=0)
is not the difficult part of this quantum simulation. One would
probably form the initial wavefunction as a product of a vibrational
function yv (r) appropriate for
the vth level of the BC molecule, a rotational
wavefunction exp(iPb
b) describing rotation of the BC
molecule, and a relative-motion wavefunction yR
(R) describing motion along the R- coordinate and a function
exp(iPaa) describing the
angular momentum of A relative to the center of mass of the BC
molecule :
y(R,r,a,b;t=0)
= yv (r ) exp(iPb
b) exp (iPa
a) yR
(R).
If, alternatively, the initial value of the total angular momentum
is specified, the relation
LZ = m' R2  -
m r2
-
m r2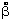 = Pa -
Pb
= Pa -
Pb
can be used to eliminate the initial Pa
and express it in terms of Lz and Pb
.
The most likely way to describe a collision in which the A atom
begins at a position R0 along the R- axis and with a
relative collision momentum along this coordinate of - PR
0 is to use a so-called coherent wave packet
function (see Professor Rick
Heller):
yR (R) = exp
(-iPR0 R/h)
[2p <dR>2
]-1/2 exp (-(R-R0 )2
/(4<dR>2 )).

Professor Rick Heller
Here, the parameter <dR>2
gives the uncertainty or "spread" along the R- degree of freedom for
this wavefunction, defined as the mean squared displacement away from
the average coordinate R0 , since it can be shown for the
above function that
Ú
(R-R0)2 yR*
(R) yR (R) R2
dR = <dR>2
and that
R0 = Ú R
yR *(R) yR
(R) R2 dR.
It can also be shown that the parameter PR0
is equal to the average value of the momentum along the R
coordinate:
Ú yR (R)*{-
i h  yR/
yR/ R
} R2 dR = PR0,
R
} R2 dR = PR0,
and that the uncertainty in the momentum along the R
coordinate:
<dPR2>
= Ú yR (R)*{- i
h  yR
yR R
+ PR0 yR
(R) }2 R2 dR
R
+ PR0 yR
(R) }2 R2 dR
is related to the uncertainty in the R-coordinate by
<dPR2>
<dR2 > =
h2/4.
Note that for these coherent state wavefunctions, the
uncertainties fulfill the general Heisenberg uncertainty criterion
for any coordinate Q and its conjugate momentum P:
<dP2>
<dQ2> >
h2/4
but have the smallest possible product of uncertainties. In this
sense, the coherent state function is the closest possible to a
classical description (where uncertainties are absent).
II. Time propagation of the wavefunction must
be effected- the basis expansion approach
The difficult part of the propagation process involves applying
the time evolution operator exp (- iHt/h) to this
initial wavefunction. The most powerful tools for applying this
operator fall under the class of methods termed Feynman path-integral
methods (see the links to Professors Greg
Voth, Nancy
Makri, and Jim
Doll). However, let us first examine an approach that has
been used for a longer time, for example in the hands of Professors
George Schatz
and John
Light.

|
|

|
|
Professor Greg Voth
|
|
Professor Nancy Makri
|

|
|

|
|
Professor George Schatz
|
|
Professor John Light
|
|
|

|
|
|
|
Professor Jim Doll
|
|
Several other first-rate theorists have contributed much to the
field of molecular dynamics, including quantum dynamics and
condensed-media processes. They include those shown below:

Professor Chi
Mak, USC

Professor Debbie
Evans, University of New Mexico

Professor David
Freeman, University of Rhode Island

Professor Ann
McKoy, Ohio State University

Professor Ron
Elber, Cornell Universtiy

Professor David
Wales, Cambridge University

Professor Rob
Coalson, University of Pittsburgh, one of the leaders in the
applications of quantum dynamics to condensed phase and biological
problems including ion channels.
a. Expanding the wavefunction in a basis
If, alternatively, one prefers to attempt to solve the
time-independent Schrödinger equation Hyk
= Ek yk the most
widely used approaches involve expanding the unknown y(R,r,a,b)
in a basis consisting of products of functions of R, functions of r,
and functions of a and of b:
yk = Sn,v,L,M
Ck (n,v,L,M) Fn (R) yv(r)
yL (b)
yM (a).
This expansion is what one would use in the case of a non-reactive
collision. If a chemical reaction (e.g., A + BC Æ
AB + C) is to be examined, then one must add to the sum of
terms given above another sum which contains products of functions of
the so-called exit-channel coordinates (r,
t, g, and
f). In this case, one uses
yk = Sn,v,L,M
Ck (n,v,L,M) Fn (R) yv(r)
yL (b)
yM (a)
+ Sn,v,L,M
Ck (n,v,L,M) Fn (r)
yv(t)
yL (g)
yM (f).
Of course, the yv ,
yL, Fn, and
yM functions relating to the
exit-channel are different than those for the entrance channel (e.g.,
yv (r)
would be a AB-molecule vibrational wavefunction, but yv
(r) would be a BC-molecule vibrational function).
As will be seen from the discussion to follow shortly, expanding
y in this manner and substituting into the
Schrödinger equation produces a matrix eigenvalue equation whose
eigenvalues are the Ek and the eigenvectors are the
expansion coefficients Ck (n,v,L,M). Given any
wavefunction y(R,r,a,b;t=0)
at t=0 (e.g., the one shown above may be appropriate for a collision
of A with a BC molecule in a specified vibrational/rotational state),
one can then express this wavefunction at later times as follows:
y(R,r,a,b;t)
= Sk yk
exp(-i Ekt/h) yk
* y(R,r,a,b;t=0)
dr .
This expression arises when one uses the facts that:
1. the {yk } form a complete
set of functions so one can expand y(R,r,a,b;t=0)
in this set, and
2. the time evolution operator exp (-i Ht/h) can
be applied to any eigenfunction yk
and produces exp (-i Ht/h) yk
= exp (-i Ekt/h) yk
.
So, it is possible to follow the time development of an initial
quantum wavefunction by first solving the time-independent
Schrödinger equation for all of the {yk
} and then expressing the initial wavefunction in
terms of the eigenfunctions (i.e, the integral Ú
yk * y(R,r,a,b;t=0)
dr is nothing but the expansion coefficient of y(R,r,a,b;t=0)
in terms of the yk ) after
which the wavefunction at a later time can be evaluated by the
expression
y(R,r,a,b;t)
= Sk yk
exp(-i Ekt/h) Ú
yk * y(R,r,a,b;t=0)
dr.
b. The resulting matrix eigenvalue problem
Let us now return to see how the expansion of y
in the manner
yk = Sn,v,L,M
Ck (n,v,L,M) Fn (R) yv(r)
yL (b)
yM (a)
(or the generalization in which both entrance- and exit-channel
product functions are used) produces a matrix eigenvalue problem.
Substituting this expansion into Hy
=Ey and subsequently multiplying through
by the complex conjugate of one particular Fn' (R)
yv' (r) yL'
(b) yM'
(a)and integrating over R, r,
b, and a one
obtains a matrix eigenvalue equation:
H Ck = Ek
Ck
in which the eigenvector is the vector of expansion coefficients
Ck (n.v,L,M) and the H matrix has elements
H(n,v,L,M|n',v',L',M')
= < Fn' (R) yv'
(r) yL' (b)
yM' (a)| H | Fn
(R) yv(r) yL
(b)
yM (a)>
given in terms of integrals over the basis functions with the
above Hamiltonian operator in the middle. Notice that in writing the
integral on the right-hand side of the above equation, the so-called
Dirac notation has been used. In this notation, any integral with a
wavefunction on the right, a complex conjugated wavefunction on the
left, and an operator in the middle is written as follows:
ÚY*Opfdq
= < Y|Op|f>
c. The dimension of the matrix scales as the number of basis
functions to number of coordinates power
What makes the solution of the four-variable Schrödinger
equation much more difficult than the propagation of the
four-coordinate (plus four-momenta) Newtonian equations? The
Hamiltonian differential operator
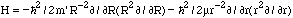
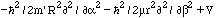
is non-separable because V depends on R, r, and q
(which is related to b and a
by q = a +
b ) in a manner that can not be broken
apart into an R-dependent piece plus an r-dependent piece plus a
q-dependent piece. As a result, the four
dimensional second-order partial differential equation can not be
separated into four second-order ordinary differential equations.
This is what makes its solution especially difficult.
To make progress solving the four-dimensional Schrödinger
equation on a computer, one is thus forced either to
1. expand y (R,r,a,b)
as S C(n,v,L,M) Fn (R)
yv(r) yL
(b) yM
(a), and then solve the resultant
matrix eigenvalue problem, or to
2. represent y (R,r,a,b)
on a grid of points in R, in r, and in a
and b space and use
finite-difference expressions (such as [F(R+dR)
+ F(R-dR) -2F(R)]/d2
to represent d2F(R)/dR2 ) to also express
the derivatives on this same grid to ultimately produce a sparse
matrix whose eigenvalues must be found.
In either case, one is left with the problem of finding
eigenvalues of a large matrix. In, the former case, the dimension of
the H matrix is equal to the product of the number of Fn
(R) functions used in the expansion times the number of
yv(r) functions used times the
number of yL (b)
used and times the number of yM
(a) functions. In the latter case,
the dimension of H is equal to the number of grid points along
the R coordinate times the number of grid points along r times the
number along b and times the number along
a. It is the fact that the dimension of
H grows quartically with the size of the basis or grid set
used (because there are four coordinates in this problem; for a
molecule with N atoms, the dimension of H would grow as the
number of grid points or basis functions to the 3N-6 power!) and that
the computer time needed to find all of the eigenvalues of a matrix
grows as the cube of the dimension of the matrix (to find one
eigenvalue requires time proportional to the square of the dimension)
that makes the solution of this quantum problem very difficult.
Let us consider an example. Suppose that a grid of 100 points
along the R-coordinate and 100 points along the r-coordinate were
used along with say only 10 points along the a
and b-coordinates. This would produce a
(albeit very sparse) H matrix of dimension 106 . To
find just one eigenvalue of such a large matrix on a 100 Mflop
desktop workstation would require of the order of several times
(106)2 /(100x106 ) sec, or at least
100 minutes. To find all 106 eigenvalues would require
106 times as long.
III. Time propagation of the wavefunction
can be effected using Feynman path integrals instead
Given a wavefunction at t=0, y(R,r,a,b;t=0),
it is possible to propagate it forward in time using so-called path
integral techniques that Richard
Feynman pioneered and which have become more popular and
commonly used in recent years (see links to Professors Greg
Voth, Jim
Doll, and Nancy
Makri). In these approaches, one divides the time interval
between t=0 and t=t into N small increments of length t
= t/N, and then expresses the time evolution operator as a product of
N short-time evolution operators:
exp[-i Ht/h ] = {exp[-i
Ht/h ]}N
.
For each of the short time steps t ,
one then approximates the propagator as
exp[-i Ht/h]
= exp[-i Vt/2h]
exp[-i Tt/h]
exp[-i Vt/2h],
where V and T are the potential and kinetic energy operators that
appear in H = T + V. It is possible to show that the above
approximation is valid up to terms of order t4
. So, for short times (i.e., small t
), these so-called symmetric split operator approximations to the
propagator should be accurate.
The time evolved wavefunction y (t) can
then be expressed as
y (t) = { exp[-i
Vt/2h] exp[-i
Tt/h] exp[-i
Vt/2h]}N
y (t=0).
The potential V is (except when external magnetic fields are
present) a function only of the coordinates {qj } of the
system, while the kinetic term T is a function of the momenta
{pj } (assuming cartesian coordinates are used). By making
use of the completeness relations for eigenstates of the coordinate
operator
1 =  dqj|
qj> <
qj|
dqj|
qj> <
qj|
and inserting this identity N times (once between each power of
exp[-i Vt/2h]
exp[-i Tt/h]
exp[-i Vt/2h]),
the expression given above for y (t) can
be rewritten as follows:
y (qN ,t)=
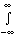 dqN-1
dqN-2 . . . dq1 dq0
dqN-1
dqN-2 . . . dq1 dq0 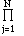 exp{(-it/2
exp{(-it/2h)[V(qj)
+ V(qj-1)]}
< qj|
exp(-itT / h
) |qj-1>y
(q0 ,0).
Then, by using the analogous completeness identity for the
momentum operator
1 = 1 / h 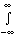 dpj|
pj>< pj |
dpj|
pj>< pj |
one can write
< qj|
exp(-itT / h
) |qj-1> = 1 /
h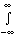
dp
< qj|p > exp(-ip2t
/ 2mh ) < p|qj-1 >.
Finally, by using the fact that the momentum eigenfunctions
|p>, when expressed as functions of coordinates q are given by
< qj|p > = (1/2p)1/2
exp(ipq/h),
the above integral becomes
< qj | exp(-itT
/ h) |qj-1> = 1/2 ph
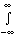 dp
exp(-ip2 t /
2m
dp
exp(-ip2 t /
2mh) exp[ip(qj - qj -
1)].
This integral over p can be carried out analytically to give
< qj | exp(-itT
/ h) |qj-1> =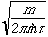 exp[im(qj
- qj - 1)2 /
2
exp[im(qj
- qj - 1)2 /
2ht].
When substituted back into the multidimensional integral for
y (qN ,t), we obtain
y (qN ,t)=
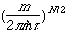
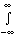 dqN-1
dqN-2 . . . dq1 dq0
dqN-1
dqN-2 . . . dq1 dq0
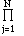 exp{(-it/2
exp{(-it/2h)[V(qj)
+ V(qj-1)]}
exp[im(qj
- qj-1)2
/2ht]
y (qo,0)
or
y (qN ,t) = 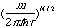
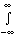 dqN-1
dqN-2 . . . dq1 dq0
exp{i/
dqN-1
dqN-2 . . . dq1 dq0
exp{i/h 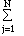 [m(qj
- qj-1)2 / 2t
- t(V(qj)
+ V(qj-1))/2]} y (q0
, t=0).
[m(qj
- qj-1)2 / 2t
- t(V(qj)
+ V(qj-1))/2]} y (q0
, t=0).
Why are such quantities called path integrals? The sequence of
positions q0 , q2 , ... qN describes
a "path" connecting q0 to qN . By integrating
over all of the intermediate positions q1 , q2
,... qN-1 one is integrating over all such
paths.
Further insight into the meaning of the above is gained by first
realizing that
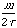 (qj
- qj-1)2 =
(qj
- qj-1)2 = 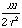 (qj
- qj-1)2 t
=
(qj
- qj-1)2 t
= 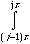 Tdt
Tdt
is the representation, within the N discrete time steps of length
t, of the integral of Tdt over the
jth time step,
and that
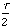 [V(qj)
+ V(qj-1)] =
[V(qj)
+ V(qj-1)] = 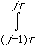 V(q)dt
V(q)dt
is the representation of the integral of Vdt over the jth
time step. So, for any particular path (i.e., any specific set
of q0 , q1, , ... qN-1 , qN
values), the sum over all N such terms 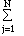 [m(qj
- qj-1)2 / 2t
- t(V(qj) +
V(qj-1))/2]
[m(qj
- qj-1)2 / 2t
- t(V(qj) +
V(qj-1))/2]
is the integral over all time from t=0 until t=t of the so-called
Lagrangian L = T - V:
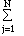 [m(qj
- qj-1)2 / 2t
- t(V(qj) +
V(qj-1))/2] =
[m(qj
- qj-1)2 / 2t
- t(V(qj) +
V(qj-1))/2] = 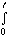 Ldt.
Ldt.
This time integral of the Lagrangian is called the "action" S in
classical mechanics. Hence, the N-dimensional integral in terms of
which y (qN ,t) is expressed
can be written as
y (qN ,t) =
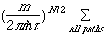 exp{i
/
exp{i
/ h  dt
L } y (q0 ,t=0).
dt
L } y (q0 ,t=0).
Here, the notation "all paths" is realized in the earlier version
of this equation by dividing the time axis from t=0 to t=t into N
equal divisions, and denoting the coordinates of the system at the
jth time step by qj . By then allowing each
qj to assume all possible values (i.e., integrating over
all possible values of qj ), one visits all possible paths
that begin at q0 at t=0 and end at qN at t=t.
By forming the classical action S
S =  dtL
dtL
for each path and then summing exp(iS/h)
y ( q0 , t=0)
over all paths and multiplying by 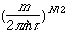 ,
,
one is able to form y (qN
,t).
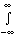 dqN-1
dqN-2 . . . dq1 dq0
exp{i/
dqN-1
dqN-2 . . . dq1 dq0
exp{i/h 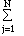 [m(qj
- qj-1)2 / 2t
- t(V(qj)
+ V(qj-1))/2]}
[m(qj
- qj-1)2 / 2t
- t(V(qj)
+ V(qj-1))/2]}
The difficult step in implementing this Feynman path integral
method in practice involves how one identifies all paths connecting
q0 , t=0 to qN , t. Each path contributes an
additive term involving the complex exponential of the quantity
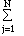 [m(qj
- qj-1)2 / 2t
- t(V(qj) +
V(qj-1))/2]
[m(qj
- qj-1)2 / 2t
- t(V(qj) +
V(qj-1))/2]
This sum of many, many (actually, an infinite number) oscillatory
exp(iS/h) = cos (S/h) + i
sin(S/h) terms is extremely difficult to evaluate
because of the tendency of contributions from one path to cancel
those of another path. The evaluation of such sums remains a very
active research subject. The most commonly employed approximation to
this sum involves finding the path(s) for which the action
S= 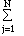 [m(qj
- qj-1)2 / 2t
- t(V(qj) +
V(qj-1))/2]
[m(qj
- qj-1)2 / 2t
- t(V(qj) +
V(qj-1))/2]
is smallest because such paths produce the lowest frequency
oscillations in exp(iS/h), and thus are not subject
to cancellation by contributions from other paths.
The path(s) that minimize the action S are, in fact the classical
paths. That is, they are the paths that the system whose quantum
wavefunction is being propagated in time would follow if the system
were undergoing classical Newtonian mechanics subject to the
conditions that the system be at q0 at t=0 and at qN
at t=t. In this so-called semi-classical approximation to the
propagation of the initial wavefunction using Feynman path integrals,
one finds all classical paths that connect q0 at t=0 and
at qN at t=t, and one evaluates the action S for each such
path. One then applies the formula
y (qN ,t) =
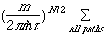 exp{i
/
exp{i
/ h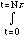 dt
L } y (q0 ,t=0)
dt
L } y (q0 ,t=0)
but includes in the sum only the contribution from the classical
path(s). In this way, one obtains an approximate quantum propagated
wavefunction via a procedure that requires knowledge of only
classical propagation paths.
b. How is information extracted from a quantum
dynamics simulation?
Once an initial quantum wavefunction has been propagated for a
time long enough for the event of interest to have occurred (e.g.,
long enough for an A + BC Æ AB + C
reactive collision to take place in the above example problem), one
needs to interpret the wavefunction in terms of functions that are
applicable to the final-state. In the example considered here, this
means interpreting y(R, r, a,
b; t) in terms of exit-channel basis
states that describe an intact AB molecule with a C atom moving away
from it (i.e., the terms Sn,v,L,M
Ck (n,v,L,M) Fn (r)
yv(t)
yL (g)
yM (f)).
As explained earlier when the classical trajectory approach was
treated, to describe this final-state configuration of the three
atoms, one uses different coordinates than R,r,a,b
that were used for the initial state. The appropriate coordinates are
shown below in the figure.
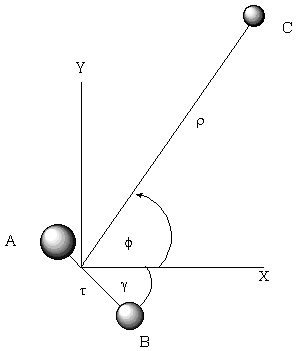
That is, one projects the long-time wavefunction
y(R,r,a,b;t)
= Sk yk
exp(-i Ekt/h) Ú
yk * y(R,r,a,b;t=0)
dr
onto a particular exit-channel product function Fn
(r) yv(t)
yL (g)
yM (f)
to obtain the amplitude A of that exit channel in the final
wavefunction:
A = < Fn (r)
yv(t)
yL (g)
yM (f)|
y(R,r,a,b;t)>
= Sk < Fn
(r) yv(t)
yL (g)
yM (f)|
yk>
exp(-iEkt/h) Ú
yk * y(R,r,a,b;t=0)
dr.
Using the earlier expansion for yk
, one sees that
< Fn (r)
yv(t)
yL (g)
yM (f)|
yk> = Ck
(n,v,L,M)
for the exit channel, so the modulus squared of A, which gives the
probability of finding the AB + C system in the particular final
state
Fn (r) yv(t)
yL (g)
yM (f),
is given by:
|A|2 = | Sk
Ck (n,v,L,M) exp(-i Ekt/h)
Ú yk * y(R,r,a,b;t=0)
dr |2 .
This result can be interpreted as saying that the probability of
finding the state Fn (r)
yv(t)
yL (g)
yM (f)
is computed by (1) first, evaluating the projection of the
initial wavefunction along each eigenstate (these components
are the Ú yk *
y(R,r,a,b;t=0)
dr), (2) multiplying by the projection of the specified
final wavefunction along each eigenstate (the < Fn
(r) yv(t)
yL (g)
yM (f)|
yk> = Ck
(n,v,L,M)), (3) multiplying by a complex phase factor exp(-i
h Ek t) that details how each eigenstate
evolves in time, and (4) summing all such products after which (5)
taking the modulus squared of the entire sum.
3. Present Day Challenges in Chemical
Dynamics
In addition to the people specifically mentioned in this text for
whom I have already provided web links, I encourage you to look at
the following web pages for further information:
|

|
Professor Bill
Reinhardt, University of Washington. His early
career focused on developing theories and computational
tools for studying the dynamical decay of metastable states
(e.g., such as occurs in unimolecular decomposition of
molecules) and the rates of energy transfer among modes in
molecules.
|
|
Professor Richard
Stratt, Brown University. He has been involved in
examining the dynamics of clusters of atoms or molecules
that are small on a macroscopic level (i.e., do not contain
enough atoms to be considered to follow macroscopic
thermodynamic laws) yet large enough to show certain
characteristics (e.g., phase transition like behavior)
associated with macroscopic systems.
|

|
|

|
The late Professor Kent
Wilson, University of California, San Diego. He was
active in simulating dynamical behavior of a wide variety of
complicated chemical and physical systems. His web sites
contain some of the more "exciting" depictions and
animations of molecular phenomena.
|
|
Professor John
Tully, Yale University, has pioneered much of the
study of dynamics and reactions that occur at or near
surfaces and he invented the most commonly used so-called
surface hopping model for treating non-adiabatic transitions
among potential energy surfaces.
|
|
Professor Mark Child, Oxford University has, along with
Professor Bill Miller, Berkeley, developed the area of semi-classical
collision and reaction dynamics. This approch to solving quantum
equations in a manner that allows one to retain a great deal of
classical mechanics' conceptual clarity has been very successufl and
has lead to many new insights.

Professor Mark
Child of Oxford University

Professor Bill
Miller of Berkeley
Professor Don Truhlar, University of Minnesota was able to extend
the Eyring idea of the transition state (the "pass" or col separating
reactant and product valleys on the potential energy surface) by
introducing what is now termed Variational Transition State Theory in
which a pass on a free energy surface replaces the conventional
transition state. He and his long-time collaborator, Dr. Bruce
Garrett, succeeded in making this theory one of the most useful
computational and conceptual tools in reaction dynamics.


Don Truhlar and Bruce Garrett
Professor D
avid Clary, University College, London has extended the
capability of quantum reactive dynamics theory to systems with
several degrees of freedom by introducing clever approximations that
focus attention on certain "active" coordinates while treating other
coordinates in an approximate manner. Such approaches are essential
if one hopes to employ quantum methods on more than the simplest
chemical reactions.

Professor Bob
Wyatt, University of Texas,

has played a primary role in developing new methods and algorithms
that allow one to use quantum dynamics efficiently to study chemical
reactions and energy flow in molecules and in collsions.
Professor Herschel
Rabitz of Princeton University has worked closely with
experimentalists to show that series of specially tuned light pulses
can be used to selectively excite a molecule in a manner that allows
one to control which bond is broken.

Professor Susan
Tucker, University of California, Davis.

Professor Ned
Sibert, University of Wisconsin, has been studing intramolecular
energy flow and the interactions of lasers with small molecules. The
goal of much of this work is to determine how one might control where
the energy goes in a molecule that is photo-excited. This very
exciting branch of photochemistry is eventually aimed at trying to
control the energy (i.e., to keep it in certain internal modes) so
that one might effect the outcome (i.e., which products are formed)
of chemical reactions.

The University of Wisconsin, Madison has one of the longest
traditions of excellence in theoretical chemistry, dating back to
when the late Prof. Joseph O. Hirschfelder started the theortical
chemistry institute (TCI). Their strength in theory continues to this
day with Profs. Jim Skinner, Prof. Ned Sibert, Prof. John Harriman,
Prof. Frank Weinhold, Prof. Arun Yethiraj, and Prof. Qiang Cui shown
below.


Qiang Cui
(left), whose works focus on macromolecules such as catalysis in
enzymes or ATP hydrolysis in motor proteins, and John
Harriman (right) whose efforts have emphasized gaining a better
understanding of the electronic structure of molecules by use of
reduced density matrices.



Professor Jim
Skinner (left) whose work is discussed elsewhere and who serves
as Director of TCI, Prof. Frank
Weinhold (center) who invented the Natural Bond Orbital (NBO)
analysis methods that offer a mathematically rigorous "Lewis
structure" representation of the wavefunction, and Prof. Arun
Yethiraj, who has contributed much to the statistical mechanical
study of polyme materials.
Professor Jeff
Krause, University of Florida has been studying the interaction
of pulses of coherent electromagnetic radiation with molecules in
hopes of designing laser means for controlling which bonds are broken
in a photochemical process.

Professor John
Straub, Boston University is currently the Chair of the
Theoretical Chemistry Subdivision of the Physical Chemistry Division
of ACS. His work involves using molecular dynamics and Monte-Carlo
simulation tools to study biomolecules, liquids, and clusters.
Two of John's colleagues at Boston University are

Professor David
Coker whose group develops new methods for treating
condensed-phase chemical dynamics and

Professor Tom
Keyes whose group specializes in statistical mechanics of
supercooled liquids
a. Large Biomolecules and Polymers
Following the motions of large molecules even using classical
Newton equations involves special challenges. First, there is the
fact that large molecules contain more atoms, so the Newtonian
equations that must be solved involve many coordinates (N) and
momenta. Because the potential energy functions,and thus the
Newtonian forces, depend on the relative positions of the atoms, of
which there are N(N-1)/2 , the computer time needed to carry out a
classical trajectory varies as (at least) the square of the number of
atoms in the molecule. Moreover, to adequately sample an ensemble of
initial coordinates and momenta appropriate to a large molecule, one
needs to run many trajectories. That is, one needs to choose a range
initial values for each of the molecule's internal coordinates
and momenta; the number of such choices is proportional to N. The net
result is that computer time proportional to N3 (or worse)
is needed,and this becomes a major challenge for large biomolecules
or polymers. One way this problem is being addressed is to use
parallel computers which allow one to run trajectories with different
initial conditions on different processors.
Another problem that is special to large molecules involves the
force field itself (see, for example, the web pages of Professors
Andy McCammon,
Charles Brooks and the
late Peter
Kollman, as well as of Biosym
and CHARMm).
Usually, the potential energy is expressed as a sum of terms
involving:
1. bond stretching potentials of either harmonic V(r) = 1/2 k
(r-re)2 or Morse form V(r) = De
(1-exp(-b(r-re)))2
2. bond angle bending potentials of harmonic form depending on the
angles between any three atoms A, B, C that are bonded to one another
(e.g., the H-C-H angles in -CH2 - groups)
3. dihedral angles (e.g., the H-C-C-H angle in
-H2C-CH2- groups
4. Van der Waals interactions V(r) = Ar-12 - Br-6
among all pairs of atoms (these potentials allow for repulsions
among, for example, the H atoms of a methyl group in
H3C-CH2-CH2-CH2-CH2-C
H3 to repel the other H atoms as this "floppy" molecule
moves into geometries that bring such groups into strong steric
interaction)
5. electrostatic attraction (for opposite charges) and repulsions
(for like charges) among charged or highly polar groups (e.g.,
between pairs of phosphate groups in a biopolymer, between a Na+
ion and a phosphate group, or between a charged group and a
neighboring H2O molecule)
6. polarization of the electronic clouds of the large solute
molecule or of surrounding solvent molecules induced by ionic or
highly polar groups approaching highly polarizable parts of the
molecule.
|

|
|

|
|
Professor Andy McCammon
|
|
The Late Professor Peter Kollman
|

Professor Charles Brooks
Professor Joan-Emma
Shea, University of California, Santa Barbara, has been studying
bio-molecules folding and motions as well.

Professor Joan Shea, University of California, Santa
Barbara
Professor
Klaus Schulten (below) University of Illinois Physics, has
studied many problems in biophysics. Most recently, he has focued
on the structure and function of supramolecular systems in the
living cell, and on the development of non-equilibrium statistical
mechanica
descriptions and efficient computing tools for structural
biology.

Professor Zan
Luthey-Schulten, University of Illinois Chemistry is one of the
world's leading figures in using statistical mechancis techniques
to predict protein structures and to understand their relations to
their functions.

One of the earliest pioneers in applying fundamental statistical
mechanics, molecular mechanics, and solvation modelling theories to
bio-molecules is Professor Arieh Warshel (below). His groups more
recent interests include the dynamics of photobiological processes,
enzyme catalysis and protein action, as well as the study of basic
chemical reactions in solutions.

Professor Arieh Warshel,
University of Southern Califonia

Professor Jeffry
Madura, Duquesne Universtiy
The primary difficulties in using such a multi-parameterized force
field are
1. that the values of the parameters characterizing each kind of
potential have to be obtained either by requiring the results of a
simulation to "fit" some experimental data or by extracting these
parameters from ab initio quantum chemical calculations of the
interaction potentials on model systems;
2. these developments and calibrations of the parameters in such
force fields are still undergoing modifications and improvements, so
they are not yet well established for a wide range of functional
groups, solvents, ionic strengths, etc.
One more difficulty that troubles most large molecule simulations
is the wide range of time scales that must be treated when solving
the Newton equations. For example, in attempting to monitor the
uncoiling of a large biomolecule, which may occur over a time scale
of ca. 10-5 to 1 sec, one is usually forced to "freeze"
the much faster motions that occur (i.e., to treat the C-H, O-H, and
N-H bonds, which oscillate over ca.10-14 sec, as rigid).
If one were to attempt to follow the faster motions, one would have
to take time steps in solving the Newton equations of ca. 10-14
sec, as a result of which the uncoiling event would require
109 to 1014 time steps. Even with a computer
that could perform 109 floating point operations per
second (i.e., a one gigaflop computer), and assuming that a single
time step would use at least 1000 floating point operations (which is
very optimistic), a single such trajectory would use 103
to 108 seconds of computer time. This is simply
unrealistic. As a result, one is forced to freeze (i.e., by
constraining to fixed geometries) the faster motions so that the
Newton equations can be solved only for the slower motions. It is an
area of current research development to invent new methods that allow
such multiple time scale issues to be handled in a more efficient and
accurate manner.
b. Mixed Classical and Quantum Dynamics
One of the most pressing issues in chemical reaction dynamics
involves how to treat a very large molecular system that is
undergoing a chemical reaction or a photochemical event (i.e., a
change that affects its electronic structure). Because the
system's bonding and other attributes of its electronic wavefunction
are changing during such a process, one is required to use quantum
mechanical methods. However, such methods are simply impractical
(because their computer time, memory, and disk space needs scale as
the number of electrons in the system to the fourth (or higher)
power) to use on very large molecules.
If the chemical reaction and/or photon excitation is localized
within a small portion of the molecular system (that may involve
solvent molecules too), there are so-called quantum
mechanics/molecular mechanics (QMMM) methods currently under much
development that can be employed. In these methods, one uses an
explicit quantum chemical (ab initio or semi-empirical) method
to handle that part of the system that is involved in the electronic
process. For example, in treating the tautomerization of
formamide H2 N-CHO to formamidic acid HN=CHOH in
aqueous solution,
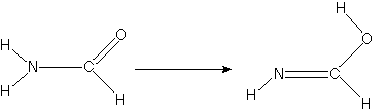
one must treat the six atoms in the formamide explicitly using
quantum chemistry tools. The surrounding water molecules
(H2O)n could then be handled using a classical
force field (i.e., the formamide-water and water-water interaction
potentials as well as the internal potential energy function of each
H2O molecule could be expressed as a classical potential
like those described earlier in this section). If, on the other hand,
one wished to treat one or more of the H2O solvent
molecules as actively involved in promoting the tautomerization (as
shown in the figure below)
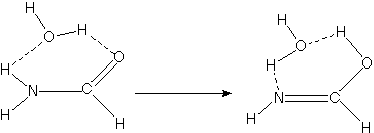
one would use quantum chemistry tools to handle the formamide plus
the actively involved water molecule(s), and use classical potentials
to describe the interactions of the remaining solvent molecules with
these active species and among one another. At present, much effort
is being devoted to developing efficient and accurate ways to combine
quantum treatment of part of the system with classical treatment of
the remainder of the system. Professor Chris Cramer has been very
active developing new ways to model the influence of surrounding
solvent molecules on chemical species whose spectroscopy or reactions
one wishes to study.

Chris
Cramer
Professors Mark
Gordon, Than
h Truong, Weito
Yang, and Keji
Morokuma are especially active in developing this kind of
QMMM methods. Professor Truong has made some of his programs that
compute rates of chemical reactions available through a web site
called TheRate.

|
|

|
|
Professor Mark Gordon
|
|
Professor Thanh Truong
|

Professor Keiji Morokuma
c. The Car-Parrinello Method
As discussed earlier, it is often important to treat the
electronic degrees of freedom, at least for the electrons involved in
a chemical reaction or in a photon absorption or emission event, at a
quantum level while still, at least for practical reasons, treating
the time evolution of the nuclei classically. A novel approach
developed by Car and Parrinello, and reviewed very nicely by
Remler and Madden,
incorporates the task of optimizing the electronic wavefunction into
the Newtonian dynamics equations used to follow the nuclear
movements.
The LCAO-MO coefficients Ci,k relating molecular
orbital fi to atomic orbital
ck are assumed to minimize an
energy function E[{Ci,k}] which can be a
Hartree-Fock or DFT-type function, for example. At each time step
during which the Newtonian equations
ma d2Xa /dt2
= -  E/
E/ Xa
Xa
are propagated, a corresponding propagation equation is used to
follow the time evolution of the {Ci,k } coefficients.
The latter equation was put forth by Car and Parrinello by
defining a (fictitious) kinetic energy
T = Si, k 1/2
m |dCi,k/dt|2
in which the time derivatives of the Ci,k
coefficients are viewed as analogs to the time rate of
changes of the molecule's Cartesian coordinates {Xa},
and m is a (fictitious mass introduced
to give this expression the units of energy. Then, using the
dependence of the electronic energy E on the {Ci,k } to
define the potential energy
V = E[{Ci,k}],
and then introducing a (fictitious) Lagrangian L = T-V whose
classical action S = Ú L dt is
made stationary with respect to variations in the {Ci,k
} coefficients but subject to the constraint that the
orbitals {fi} remain
orthonormal:
di,j =
S k,l C*i,k
Sk,l Cj,l
the following dynamical equations are obtained for the
Ci,k coefficients:
m d2Ci,k
/dt2 = - E/
E/ Ci,k
- Sj,l li,j
Sk,. Cj,l .
Ci,k
- Sj,l li,j
Sk,. Cj,l .
The left hand side of this equation gives the mass m
multiplied by the "acceleration" of the Ci,k variable.
The right side gives the "force" - E/
E/ Ci,k
acting on this variable, and - Sj,l
li,j Sk,.
Cj,l is the coupling force that connects
Ci.k to the other Cj,l variables (this term
arises, with its Lagrange multipliers li,j
, from the constraints di,j
= S k,l C*i,k
Sk,l Cj,l relating to the
orthonormality of the molecular orbitals. The result is that the
time evolution of the Ci,k coefficients can be followed
by solving an equation that is exactly the same in form as the
Newtonian equations ma d2Xa
/dt2 = -
Ci,k
acting on this variable, and - Sj,l
li,j Sk,.
Cj,l is the coupling force that connects
Ci.k to the other Cj,l variables (this term
arises, with its Lagrange multipliers li,j
, from the constraints di,j
= S k,l C*i,k
Sk,l Cj,l relating to the
orthonormality of the molecular orbitals. The result is that the
time evolution of the Ci,k coefficients can be followed
by solving an equation that is exactly the same in form as the
Newtonian equations ma d2Xa
/dt2 = -  E/
E/ Xa
used to follow the nuclear positions. Of course, one wonders
whether the idea used by Car and Parrinello to obtain the
classical-like equations for the time development of the Ci,k
coefficients is valid. These equations were obtained by
making stationary, subject to orthonormality constraints, an
action. However, if one were to set the mass m
equal to zero, the Lagrangian L would reduce to L = T-V = -V,
since the (fictitious) kinetic energy would vanish. Since the
Ci,k coefficients, in a conventional quantum chemical
study, would be chose to make E[{Ci.k }]
stationary, it can be shown that making the action stationary when
T vanishes is equivalent to making V stationary, which, in turn,
makes E[{Ci,k}] stationary. So, the
Car-Parrinello approach is valid, but one has to be aware of the
restriction to the ground-state
Xa
used to follow the nuclear positions. Of course, one wonders
whether the idea used by Car and Parrinello to obtain the
classical-like equations for the time development of the Ci,k
coefficients is valid. These equations were obtained by
making stationary, subject to orthonormality constraints, an
action. However, if one were to set the mass m
equal to zero, the Lagrangian L would reduce to L = T-V = -V,
since the (fictitious) kinetic energy would vanish. Since the
Ci,k coefficients, in a conventional quantum chemical
study, would be chose to make E[{Ci.k }]
stationary, it can be shown that making the action stationary when
T vanishes is equivalent to making V stationary, which, in turn,
makes E[{Ci,k}] stationary. So, the
Car-Parrinello approach is valid, but one has to be aware of the
restriction to the ground-state
(since E[{Ci,k }] is made stationary with no
constraint of orthogonality to lower-energy states) and one must
realize that finite-time-step propagations with non-zero
m render the {Ci,k}
amplitudes obtained via classical propagation not equivalent to
those obtained by minimizing E at each geometry.
Before closing this section on dynamics, I wish to bring to the
readers' attention several other leading researchers in this
exciting area of theoretical chemistry by showing photos of them
below.
|

|
|

|
- Professor
Sharon Hammes-Schiffer
- Penn State University.
- Sharon's group has made use of basis set
expansion approaches to follow the quantum dynamics of
light nuclei such as H and D, and has applied this
novel technique to a wide variety of biological and
condensed-phase systems.
|
|
Professor
Jan Linderberg, Aarhus University
|
C.
Statistical mechanics provides the framework for studying large
collections of molecules and tells us how to average over
positions and velocities to properly simulate the laboratory
distribution of molecules
When dealing with a sample containing a large number (e.g.,
billions) of molecules, it is impractical to attempt to monitor
the time evolution of the coordinates and momenta (or analogous
quantum state populations) of the individual constituent
molecules. Especially for systems at or near equilibrium, these
properties of individual molecules may vary irregularly on very
short time scales (as the molecules undergo frequent collisions
with neighbors), but the average behavior (e.g, average
translational energy or average population of a particular
vibrational energy level) changes much more gently with time. Such
average properties can be viewed as averages for any one molecule
over a time interval during which many collisions occur or as
averages over all the molecules in the sample at any specific
time.
By focusing on the most probable distribution of the total
energy available to a sample containing many molecules and by
asking questions that relate to the average properties of the
molecules, the discipline of statistical mechanics provides a very
efficient and powerful set of tools (i.e., equations) for
predicting and simulating the properties of such systems. In a
sense, the machinery of statistical mechanics allow one to
describe the "most frequent" behavior of large molecular systems;
that is how the molecules are moving and interacting most of the
time. Fluctuations away from this most probable behavior can also
be handled as long as these fluctuations are small.
1. The framework of statistical mechanics
provides efficient equations for computing thermodynamic
properties from molecular properties
a. The Boltzmann population equation
The primary outcome of asking what is the most probable
distribution of energy among a large number N of molecules within
a container of volume V that is maintained at a specified
temperature T is the most important equation in statistical
mechanics, the Boltzmann population formula:
Pj = Wj
exp(- Ej /kT)/Q,
where Ej is the energy of the jth quantum
state of the system (which is the whole collection of N
molecules), T is the temperature in K, Wj
is the degeneracy of the jth state, and the
denominator Q is the so-called partition function:
Q = Sj
Wj exp(- Ej
/kT).
The classical mechanical equivalent of the above quantum
Boltzmann population formula for a system with M coordinates
(collectively denoted q and M momenta denoted p)
is:
P(q,p) = h-M exp (-
H(q, p)/kT)/Q,
where H is the classical Hamiltonian, and the partition
function Q is
Q = h-M Ú
exp (- H(q, p)/kT) dq dp .
b. The limit for systems containing many
molecules
Notice that the Boltzmann formula does not say that only those
states of a given energy can be populated; it gives non-zero
probabilities for populating all states from the lowest to the
highest. However, it does say that states of higher energy Ej
are disfavored by the exp (- Ej /kT) factor, but
if states of higher energy have larger degeneracies Wj
(which they usually do), the overall population of such
states may not be low. That is, there is a competition between
state degeneracy, which tends to grow as the state's energy grows,
and exp (-Ej /kT) which decreases with increasing
energy. If the number of particles N is huge, the degeneracy
W grows as a high power (say M) of E
because the degeneracy is related to the number of ways the energy
can be distributed among the N molecules; in fact, M grows at
least as fast as N. As a result of W
growing as EM , the product function P(E) = EM
exp(-E/kT) has the form shown below (for M=10).
By taking the derivative of this function P(E) with respect to
E, and finding the energy at which this derivative vanishes, one
can show that this probability function has a peak at E* = MkT,
and that at this energy value,
P(E*) = (MkT)M exp(-M),
By then asking at what energy E' the function P(E) drops to
exp(-1) of this maximum value P(E*)
P(E') = exp(-1) P(E*),
one finds
E' = MkT (1+ 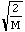 ).
).
So the width of the P(E) graph, measured as the change in
energy needed to cause P(E) to drop to exp(-1) of its maximum
value divided by the value of the energy at which P(E) assumes
this maximum value is
(E'-E*)/E* =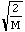 .
.
This width gets smaller and smaller as M increases. So, as the
number N of molecules in the sample grows, which causes M to grow
as discussed earlier, the energy probability functions becomes
more and more sharply peaked about the most probable energy
E*.
It is for the reasons just shown that for so-called macroscopic
systems, in which N (and hence M) is extremely large (i.e.,
10L with L being ca. 10-24), only the most probable
distribution of the total energy among the N molecules need be
considered that the equations of statistical mechanics are so
useful. Certainly, there are fluctuations (as evidenced by the
finite width of the above graph) in the energy content of the
molecular system about its most probable value. However, these
fluctuations become less and less important as the system size
(i.e., N) becomes larger and larger.
c. The connection with thermodynamics
What are some of these equations? The first is the fundamental
Boltzmann population formula shown earlier:
Pj = Wj
exp(- Ej /kT)/Q.
Using this result, it is possible to compute the average energy
<E> of a system
<E> = Sj
Pj Ej ,
and to show that this quantity can be recast (try to do this
derivation; it is not that difficult) as
<E> = kT2 ( lnQ/
lnQ/ T)N,V
.
T)N,V
.
If the average pressure <p> is defined as the pressure of
each quantum state
pj = ( Ej
/
Ej
/ V)N
V)N
multiplied by the probability Pj for accessing that
quantum state, summed over all such states, one can show that
<p> = Sj
( Ej
/
Ej
/ V)N
Wj exp(- Ej
/kT)/Q
V)N
Wj exp(- Ej
/kT)/Q
= kT( lnQ/
lnQ/ V)N,T
.
V)N,T
.
Without belaboring the point much further, it is possible to
express all of the usual thermodynamic quantities in terms of the
partition function Q. The average energy and average pressure are
given above; the average entropy is given as
<S> = k lnQ + kT( lnQ/
lnQ/ N)V,T
.
N)V,T
.
So, if one were able to evaluate the partition function Q for N
molecules in a volume V at a temperature T, either by summing the
quantum-state degeneracy and exp(-Ej/kT) factors
Q = Sj
Wj exp(- Ej
/kT)
or by evaluating the classical phase-space integral (phase
space is the collection of coordinates and conjugate momenta)
Q = h-M Ú
exp (- H(q, p)/kT) dq dp,
one could then compute all thermodynamic properties of the
system. This is the essence of how statistical mechanics provides
the tools for connecting the molecule-level properties, which
ultimately determine the Ej and the Wj,
to the macroscopic properties such as <E>, <S>,
<p>, etc.
2. Statistical mechanics gives
equations for probability densities in coordinate and momentum
space
Not only is statistical mechanics useful for relating
thermodynamic properties to molecular behavior but it is also
necessary to use in molecular dynamics simulations. When one
attempts, for example, to simulate the reactive collisions of an A
atom with a BC molecule to produce AB + C, it is not appropriate
to consider a single classical or quantal collision between A and
BC. Why? Because in any laboratory setting,
1. The A atoms are moving toward the BC molecules with a
distribution of relative speeds. That is, within the sample of
molecules (which likely contains 1010 or more
molecules), some A + BC pairs have low relative kinetic energies
when they collide, and others have high kinetic energies. There is
a probability distribution P(EKE ) for this relative
kinetic energy.
2. The BC molecules are not all in the same rotational (J) or
vibrational (v) state. There is a probability distribution
function P(J,v) describing the fraction of BC molecules that are
in a particular J state and a particular v state.
3. When the A and BC molecules collide with a relative motion
velocity vector v, they do not all hit "head on". Some
collisions have small impact parameter b (the closest distance
from A to the center of mass of BC if the collision were to
occur with no attractive or repulsive forces), and some have large
b-values (see below).
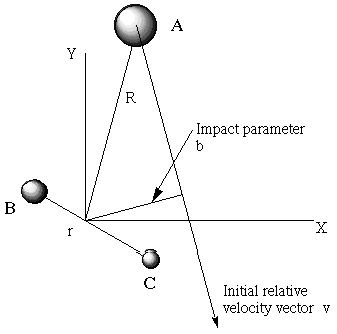
The probability function for these impact parameters is P(b) =
2p b db, which is simply a statement of
the geometrical fact that larger b-values have more geometrical
volume element than smaller b-values.
So, to simulate the entire ensemble of collisions that occur
between A atoms and BC molecules in various J, v states and having
various relative kinetic energies EKE and
impact parameters b, one must:
1. run classical trajectories (or quantum propagations) for a
large number of J, v, EKE , and b values,
2. with each such trajectory assigned an overall weighting (or
importance) of
Ptotal = P(EKE ) P(J,v)
2pb db.
3. Present Day Challenges in Statistical
Mechanics
In addition to the scientists whose work is discussed
explicitly below or later in this section, the reader is
encouraged to visit the following web sites belonging to other
leaders in the area of statistical mechanics. I should stress that
the "dividing line" between chemical dynamics and statistical
mechanics has become less clear in recent years, especially as
dynamics theory has become more often applied to condensed-media
systems containing large numbers of molecules. For this reason,
one often finds researchers who are active in the chemical
dynamics community producing important work in statistical
mechanics and vice versa.
|

|
Professor
James Skinner, University of Wisconsin. He has been a
leader in many statistical mechanics studies of glassy
materials and of relaxation processes that occur in NMR
and optical spectroscopy.
|
|
Professor
Peter Rossky, University of Texas, was one of the
earliest to use modern statistical mechanics and quantum
dynamics to study the structures and optical spectroscopy
of solvated electrons.
|

|
Professor
Hans C. Andersen, Stanford University, has pioneered many
theories and computational methodologies that describe liquids and
glasses.


Profesor Benjamin
Widom, Cornell University is one
of the world's leading figures in statistical
mechanics.
One of the most active research areas in statistical mechanics
involves the evaluation of so-called time correlation functions.
The correlation function C(t) is defined in terms of two physical
operators A and B, a time dependence that is carried by a
Hamiltonian H via exp(-iHt/h), and an equilibrium
average over a Boltzmann population exp(-bH)/Q.
The quantum mechanical expression for C(t) is
C(t) = Sj
<yj | A
exp(iHt/h) B exp(-iHt/h)
|yj >
exp(-bEj)/Q,
while the classical mechanical expression is
C(t) = Ú dq
Ú dp A(q(0),p(0))
B(q(t),p(t)) exp(-bH(q(0),p(0)))/Q,
where q(0) and p(0) are the values of all the coordinates and
momenta of the system at t=0 and q(t) and p(t) are their values,
according to Newtonian mechanics, at time t.
An example of a time correlation function that relates to
molecular spectroscopy is the dipole-dipole correlation
function:
C(t) = Sj
<yj |
e•m
exp(iHt/h) e•m
exp(-iHt/h) |yj
> exp(-bEj)/Q,
for which A and B are both the electric dipole interaction
e•m between the
photon's electric field and the molecule's dipole operator. The
Fourier transform of this particular C(t) relates to the
absorption intensity for light of frequency w:
I(w) µÚ
dt C(t) exp(iwt).
The computation of correlation functions involves propagating
either wavefunctions or classical trajectories. In the quantum
case, one faces many of the same difficulties discussed earlier in
Sec. III.B.2. However, one aspect of the task faced in the
equilibrium averaging process that is also included in C(t) makes
this case somewhat easier than in the quantum dynamics case. To
illustrate, consider the time propagation issue contained in the
quantum definition of C(t). One is faced with
1. propagating |yj >
from t=0 up to time t, using exp(-iHt/h)
|yj > and then
multiplying by B
2. propagating A+ |yj
> from t=0 up to time t, using
exp(-iHt/h)A+ |yj
>.
The exp(-bH) operator can be
combined with the first time propagation step as follows:
exp(-iHt/h) |yj
> exp(-bEj)/Q =
exp(-iHt/h) exp(-bH)
|yj >/Q
=exp(-i/h[t+bh/i]H)
|yj>/Q.
Doing so introduces a propagation in complex time from
t = 0 +bh/i
to t = t + bh/i.
The Feynman path integral techniques can now be used to carry
out this propagation. One begins, as before, by dividing the time
interval into N discrete steps
exp[-i Ht/h
] = {exp[-i Ht/Nh
]}N .
and then utilizing the same kind of short-time split propagator
methodology described earlier in our discussion of quantum
dynamics and Feynman path integrals. Unlike the real-time
propagation case, which is plagued by having to evaluate sums of
oscillatory functions, the complex-time propagations that arise in
statistical mechanics (through the introduction of t = t + bh/i)
are less problematic. That is, the quantity exp[-i Ejt/Nh
] = exp[-i Ejt/Nh ] exp[- Ejb/N] contains an
exponential "damping factor"
exp[- Ejb/N] in the complex-time case that causes the
evaluation of correlation functions to be less difficult than the
evaluation of real-time wavefunction propagation.
For a good overview of how time correlation functions relate to
various molecular properties, I urge you to look at McQuarrie's
text book on Statistical Mechanics.
Other areas of active research in statistical mechanics tend to
involve systems for which the deviations from "ideal behavior"
(e.g., dilute gases whose constituents have weak intermolecular
forces, nearly harmonic highly ordered solids, weakly interacting
dilute liquid mixtures, species adsorbed to surfaces but not
interacting with other adsorbed species, highly ordered polymeric
materials) are large. Such systems include glasses, disordered
solids, polymers that can exist in folded or disentangled
arrangements, concentrated electrolyte soltions, solvated ions
near electrode surfaces, and many more. In addition to those
scientists already mentioned above, below, I show several of the
people who are pursuing research aimed at applying statistical
mechanics to such difficult problems.

|
Professor Branka
Ladanyi, Colorado State University, has been
studying chemical reactions (including electron
transfer reactions) that occur in solutions where the
solvent interacts strongly with the reacting
species.
|
|
Professor Peter
Wolynes, University of Illinois, has contributed
much to developing new theories of how protiens and
other biopolymers undergo folding and
denaturation.
|

|
|

|
Professor
Michael Klein, University of Pennsylvania, has
used molecular dynamics and Monte-Carlo computer
simulations to study molecular overlayers, membranes,
and micelles.
|
|
Professor Doug
Henderson, Brigham Young University, is one of the
pioneers in theories of the liquid state. In
particular, he and Barker developed and made numerous
applications of perturbation theories of liquids.
|

|
Professor Hannes
Jønsson of the University of Washington has invented
numerous numerical tools for more efficiently simulating
behavior of condensed-media dynamics, in particular, liquids,
crystals, surfaces, and interfaces.

Professor JoanEmma
Shea, University of California, Santa Barbara, studies the
folding of large bio-molecules such as proteins using
Monte-Carlo and molecular dynamics methods.
Professor Tony
Haymet of the University of Houston has contributed much to
studies of hydrophobic effects and to the study of so-called
antifreeze proteins that some fish use in very cold
environments to survive.

Professor Bill
Gelbart, UCLA, uses statistical mechanics to study the
structures of very comlex fluids and to follow condensation of
DNA and other biological macromolecules.

return to title
page